Courant alternatif

• prérequis
• intensité instantanée du courant alternatif
• valeur maximum, moyenne et efficace
• 2 types de représentation
• impédance
• méthode pour traiter des circuits avec R, L et C
• puissance
• le transformateur

Prérequis

• Mathématiques : fonctions sinusoïdales, trigonométrie, vecteurs (addition)
• Electricité : électrostatique, courant continu, induction

Intensité instantanée du courant alternatif

valeur instantanée : i = I_m sin(ω . t + ε)

I_m est la valeur maximum
ω est appelé "la pulsation",
ε est appelé "la constante de phase".
L'angle (ω . t + ε) est appelé "la phase".

Le changement de signe correspond à un changement de sens du courant.

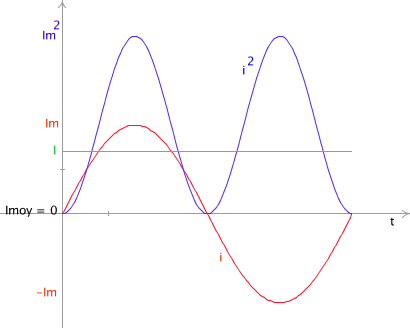
Valeur instantanée, maximum, moyenne et efficace

Les valeurs instantanées se notent avec une lettre minuscule : i, e

Elles varient entre + la valeur maximum et - la valeur maximum. Cette valeur maximum se note avec une lettre majuscule et un indice m: I_m, E_m.

La valeur moyenne sur une période est nulle : I_moy = 0, E_moy = 0.

On utilise le plus souvent la valeur efficace, qui est la valeur quadratique moyenne : la racine carrée de la moyenne du carré de la valeur instantanée.
On la note avec une lettre majuscule: I, E.
C'est la valeur efficace qu'indiquent les multimètres.

valeur efficace: \( \class{formule}{ I = \dfrac{I_m}{\sqrt{2}} }\) (lettre majuscule)

Deux types de représentations

Pour représenter le courant ou la tension, on a deux types de représentation. Soit un graphique en fonction du temps (valeur instantanée), soit la représentation de Fresnel à t = 0.

1 - représentation graphique en fonction du temps

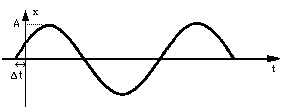
où \( \class{formule}{ Δt = - \dfrac{ε}{ω} }\)
Dans l'exemple ci-dessus, Δt < 0 ⇒ ε > 0 (avance de phase)

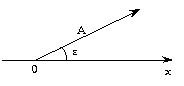
2 - représentation vectorielle de Fresnel à t = 0

C'est la représentation d'un vecteur tournant (sens trigonométrique, = sens anti-horloger) de longueur égale à la valeur maximum. La valeur instantanée est alors la projection de ce vecteur sur l'axe horizontal. On indique parfois comme longueur de ce vecteur la valeur efficace, valeur efficace et valeur maximum étant proportionnelles.

Plus de détails sur l'utilisation de ce type de représentation dans différents circuits ICI.

Impédance

impédance (Z) : \( \class{formule}{ Z = \dfrac{E_m}{I_m} = \dfrac{E}{I} }\) (= loi d'Ohm généralisée)

élément	impédance	déphasage entre E et I	Fresnel (cliquez sur le dessin pour l'agrandir)
résistance	Z = R	E et I sont en phase
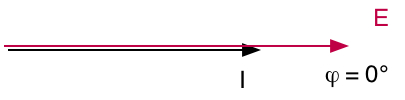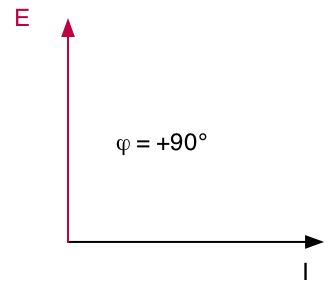
self	Z = L . ω	E est en avance de 90° sur I
condensateur	\( \class{formule}{ Z = \dfrac{1}{C . ω} }\)	E est en retard de 90° sur I

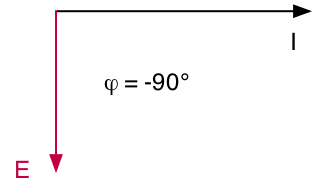Si on a un circuit composé de plusieurs éléments, voir ici comment calculer son impédance.

Résonance

• circuit RLC en série : se comporte comme un oscillateur harmonique avec excitation harmonique extérieure (revoir ici).

  pulsation propre : \( \class{formule}{ ω = \dfrac{1}{\sqrt{LC}} }\)
  résonance : Z minimum, I maximum

• circuit LC en parallèle = circuit bouchon :

  pulsation propre: \( \class{formule}{ ω = \dfrac{1}{\sqrt{LC}} }\)
  à la résonance, I = 0

Puissance

p = e . i = puissance instantanée (lettres minuscules pour les valeurs instantanées) (voir lexique)

P = E . I . cos φ = puissance moyenne (sur une période)

où φ est le déphasage entre E et I, c.à.d la différence entre les 2 phases

Comment tracer la courbe de p(t).

Le transformateur

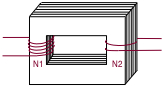
Le transformateur sert à transformer une tension alternative E₁ en une tension alternative E₂, ou encore à transformer une intensité de courant I₁ en une intensité de courant I₂.

Un transfo = 2 bobinages de N1 (primaire) et N2 (secondaire) spires. On fait passer un courant alternatif dans le primaire. Par le phénomène d'induction, cela crée une tension alternative aux bornes du secondaire. \( \class{formule}{ \dfrac{E_2}{E_1} = \dfrac{N_2}{N_1} }\) Si le secondaire fait partie d'un circuit fermé, \( \class{formule}{ \dfrac{I_2}{I_1} = \dfrac{N_1}{N_2} }\)