Electrostatique

• prérequis
• force électrique (loi de Coulomb)
• constitution de la matière
• conservation de la charge
• champ électrique
• énergie potentielle électrique, potentiel
• condensateurs
• théorème de Gauss
• dipôle électrique

Prérequis

• vecteurs (dont produit scalaire et produit vectoriel), intégrales
• dynamique du point
• dynamique du solide (concept de moment de force)
• énergie

Loi de Coulomb

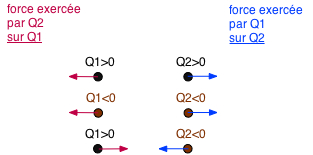
2 corps chargés de charges Q1 et Q2 ⇒ force électrique dite "de Coulomb" direction : la droite joignant ces charges sens : répulsion si mêmes signes, attraction si signes opposés grandeur : \( \class{formule} {F = \dfrac{1}{4 π ε} . \dfrac{|Q_1| . |Q_2|}{r^2} } \)

• r est la distance entre les charges,
• ε est la permittivité du milieu. Pour le vide, elle est notée ε₀, avec \( \class{formule} {\dfrac{1}{4 π ε_0} = 9 . 10^9 } \) m/farad

unité de Q : le Coulomb (C)

Constitution de la matière

matière > molécules > atomes (Q = 0) > électrons (Q < 0) + noyau (Q > 0)
noyau > nucléons > quarks

voir le schéma

ion > atome + ou - un ou plusieurs électrons (Q < 0 ou Q > 0)

Conservation de la charge

Dans un système fermé, la charge électrique totale est constante.

Champ électrique

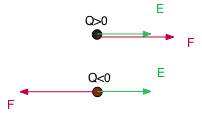
Le champ électrique est un vecteur qui caractérise l'espace près de charges électriques, tel que si on y plaçait une autre charge électrique, elle y subirait une force, la force électrique de Coulomb (mais il n'est pas nécessaire qu'il y ait une charge en un point pour qu'il y ait un champ électrique).

Si on place une charge q à l'endroit où on veut calculer £E, alors \( \class{formule}{ \vec{E} = \dfrac{\vec{F}}{q} }\)

Energie potentielle électrique

Charge q dans un champ électrique ⇒ énergie potentielle E_pot (x) = - ∫ (q . £E • dl) de (0) à x,
ou plus simplement: E_pot (x) = ∫ (q . £E • dl) de x à (0)

(0) : point où on décide arbitrairement que E_pot est nulle.

⚠️ Cette énergie potentielle électrique est parfois notée U_E. Dans ce cas, la différence de potentiel (voir plus bas) est notée ΔV au lieu de U.

Potentiel au point x

\( \class{formule}{ \class{symbol}{V(x)} = \dfrac{E_{pot}(x)}{q} = - ∫_{(0)}^{x} (\vec{E} • d\vec{l}) }\)

Unité de V : le volt (V)

La composante de £E le long d'un déplacement ds : \( \class{formule}{ E_s = - \dfrac{dV}{ds} }\)

Différence de potentiel entre 2 points A et B

U = V(B) - V(A) = - ∫_A^B (£E • dl)

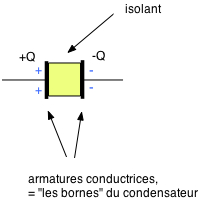
Condensateur

Condensateur plan (2 plaques parallèles) : \( \class{formule}{ C = \dfrac{ε . S}{d} }\)

• où
• S = surface des plaques,
• d = distance entre les plaques
  permittivité de l'isolant : ε = ε_r . ε₀ (ε_r, la permitivité relative, est aussi notée χ₀)

Energie contenue dans le condensateur (travail pour le charger) : W = (1/2) . C . U²

Condensateurs en série

Condensateurs placés les uns à la suite des autres, reliés uniquement par un fil conducteur sans noeud
Ils portent tous la même charge.

Cet ensemble de condensateurs équivaut à un seul condensateur ( appelé condensateur équivalent) dont la capacité vaut :

\( \class{formule}{ C = (\dfrac{1}{C_1} + \dfrac{1}{C_2} + ...)^{-1} }\)

Pour ce condensateur équivalent, U = U_tot et Q = Q₁ = Q₂ = ...

Condensateurs en parallèle

Condensateurs dont les bornes supérieures sont reliées par un fil conducteur et leurs bornes inférieures sont reliées par un autre fil conducteur.
La différence de potentiel est la même aux bornes de chacun des éléments.

Cet ensemble de condensateurs équivaut à un seul condensateur (le condensateur équivalent) dont la capacité vaut :

C = C₁ + C₂ + ...

Pour ce condensateur équivalent, Q = Q_tot et U = U₁ = U₂ = ...

Pour voir une méthode pour trouver les condensateurs en série et en parallèle, calculer le condensateur équivalent, ainsi que leur charge et leur différence de potentiel dans un circuit contenant plusieurs condensateurs, cliquez ici.

Théorème de Gauss

Le flux du champ électrique φ_E à travers une surface fermée (appelée surface de Gauss) est égal au rapport de la charge totale contenue dans cette surface à la permittivité du milieu :
\( \class{formule}{ φ_E = ∫ \vec{E} • \vec{dS} = \dfrac{Q_{int}}{ε} }\)

Pour voir une méthode pour trouver le champ électrique en utilisant le théorème de Gauss, cliquez ici.

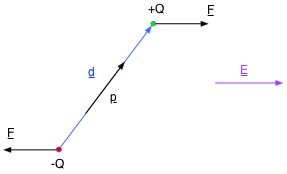
Dipôle électrique

paire de charges +Q et -Q = dipôle électrique. Dans un champ électrique ⇒ couple de forces ⇒ moment de force qui va orienter le dipôle : £M = p Λ £E p = Q . d = moment dipolaire électrique où d est le vecteur qui va de la charge -Q à la charge +Q Champs électrique d'un dipôle sur son axe : \( \class{formule} {E = \dfrac{2 . k . p}{r^3} } \) (r >> d) Champs électrique d'un dipôle sur sa médiatrice : \( \class{formule} {E = \dfrac{k . p}{r^3} } \) (r >> d) Force exercée par un gradient de champ électrique sur un dipôle : \( \class{formule} {F_x = p \dfrac{dE}{dx} } \) Energie potentielle électrique d'un dipôle : \( \class{formule} {E_{pot} = - \vec{p} • \vec{E} } \) (aussi notée UE)