Trigonométrie
- le nombre π
- le radian
- unité des angles
- cercle trigonométrique, sinus, cosinus, tangente
- quelques relations utiles
- application au triangle rectangle
- fonctions réciproques
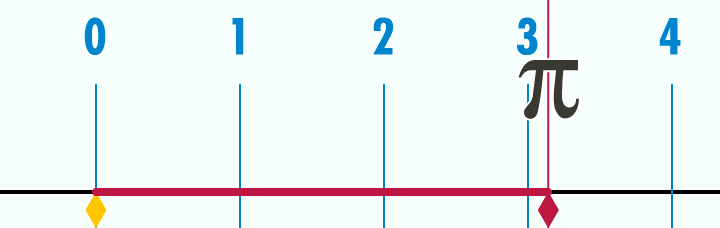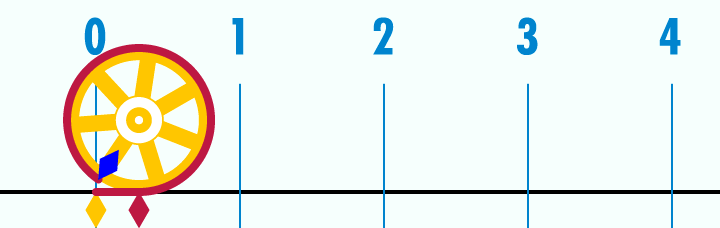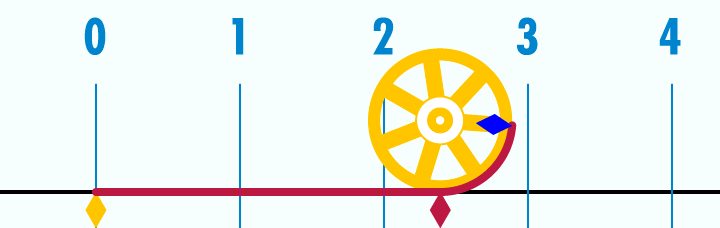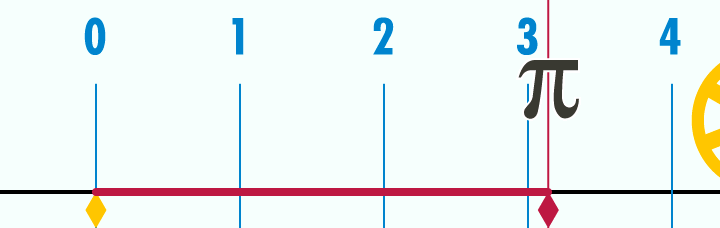
Le nombre π
C'est le rapport entre le périmètre et le diamètre d'un disque : \( \class{formule}{ π~rad = \dfrac{L}{D} }\)
Le radian
Le radian est une unité d'angle.
- Allez lire la définition.
- En images :

source
Unité des angles
Attention : travaillez-vous en radians ou en degrés ? Votre calculatrice est-elle réglée correctement ?
Pour le vérifier, si vous ne trouvez aucun signe l'indiquant, faites sin90°. Si la réponse est 1, c'est qu'elle est en degrés.
Définitions
Cercle trigonométrique (rayon 1, on tourne dans le sens antihorlogique) :
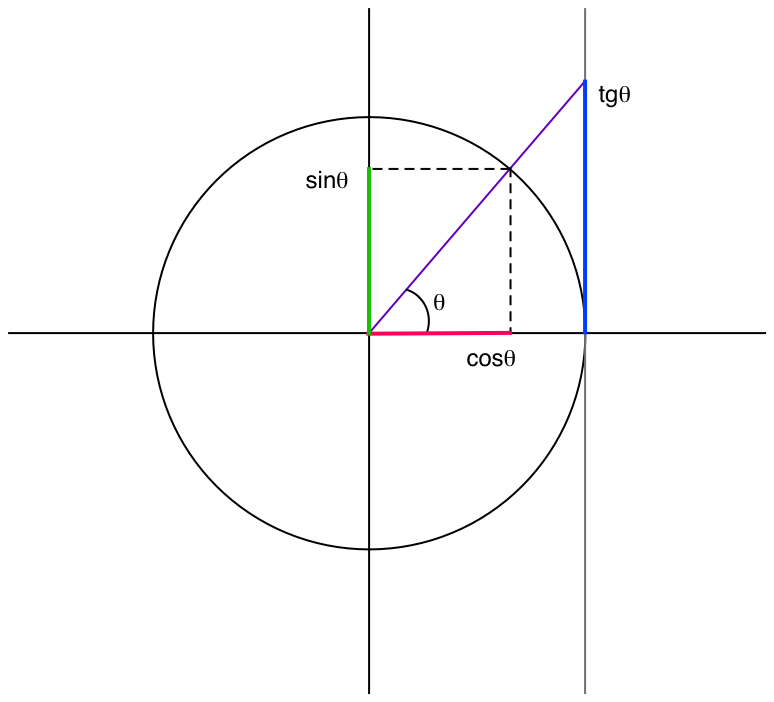 |
(Voir en correspondance avec le schéma) : sinus : côté opposé à θ cosinus : côté adjacent à θ tangente : côté opposé à θ dans le triangle obtenu en prolongeant le rayon jusqu'à la droite verticale tangente au cercle |
Le sinus et le cosinus d'un angle sont compris entre -1 et +1.
La tangente d'un angle est comprise entre -∞ et +∞.
Quelques relations utiles
\( \class{formule}{ sin^2θ + cos^2θ = 1 }\)
\( \class{formule}{ sin(θ+ φ) = sinθ . cosφ + cosθ . sinφ }\)
\( \class{formule}{ cos(θ+φ) = cosθ . cosφ - sinθ . sinφ }\)
\( \class{formule}{ tgθ = \dfrac{sinθ}{cosθ} }\)
Les relations ci-dessous peuvent être facilement retrouvées en se basant sur le cercle trigonométrique :
| \( \class{formule}{ cosθ = sin(90° - θ) }\) | \( \class{formule}{ sinθ = cos(90° - θ) }\) |
| \( \class{formule}{ sin(180° - θ) = sinθ }\) | \( \class{formule}{ cos(180° - θ) = - cosθ }\) |
| \( \class{formule}{ sin(-θ) = - sinθ }\) | \( \class{formule}{ cos(-θ) = cosθ }\) |
Application au triangle rectangle
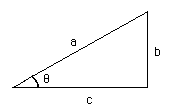 |
a est l'hypothénuse b est le côté opposé à θ c est le côté adjacent à θ |
| \( \class{formule}{ cosθ = \dfrac{c}{a} }\) ( adjacent/ hypothénuse) \( \class{formule}{ sinθ = \dfrac{b}{a} }\) (opposé / hypothénuse) ⇒ \( \class{formule}{ tgθ = \dfrac{b}{c} }\) (opposé / adjacent) |
\( \class{formule}{ a^2 = b^2 + c^2 }\) (théorème de Pythagore) |
Fonctions réciproques des fonctions sinus, cosinus et tangente
| Si x est compris entre | -1 et +1, | arcsinx = θ est un angle compris entre | -π/2 rad et +π/2 rad | tel que | sinθ = x. |
| Si x est compris entre | -1 et +1, | arccosx = θ est un angle compris entre | -π/2 rad et +π/2 rad | tel que | cosθ = x. |
| Si x est compris entre | -∞ et +∞, | arctgx = θ est un angle compris entre | -π/2 rad et +π/2 rad | tel que | tgθ = x. |