Fonctions - fonctions sinusoïdales
Prérequis
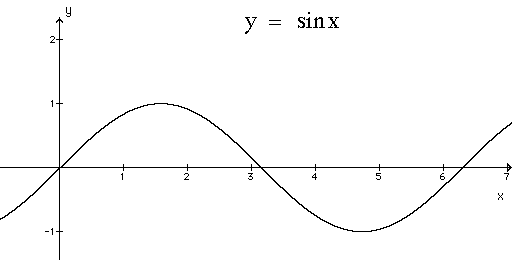
On voit que la fonction
- part de 0,
- commence à monter jusqu'à un maximum = 1 à x = π / 2 rad (environ 3,14 / 2 = 1,57 rad),
- redescend,
- pour passer par 0 à x = π rad (environ 3,14 rad),
- puis fait la même chose en négatif,
- pour revenir à 0 à x = 2 . π rad (environ 3,14 . 2 = 6,28 rad).
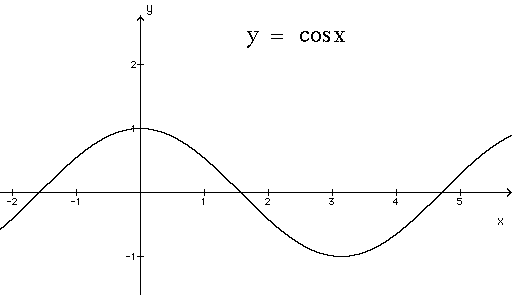
On voit que la fonction
- part de 1 (maximum),
- commence à diminuer pour passer par 0 à x = π / 2 rad (environ 3,14 / 2 = 1,57 rad),
- continue à descendre,
- jusqu'au minimum (= -1) à x = π rad (environ 3,14 rad),
- puis remonte, en passant par 0 à x = 3 . π / 2 rad (environ 3 . 3,14 / 2 = 4,71 rad)
- pour revenir à +1 à x = 2 . π rad (environ 6,28 rad).
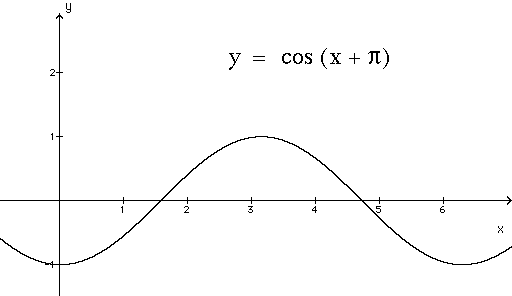
La fonction cosinus est décalée de π rad, c.à.d d'un demi cycle (un cycle : x = 2 . π rad).
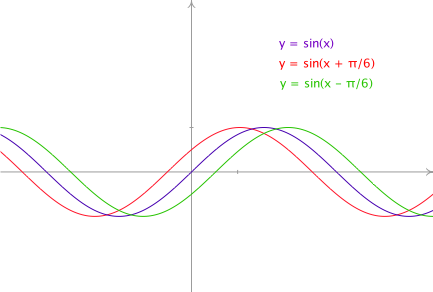
Voici
- un sinus sans déphasage (en mauve),
- un sinus avec une avance de phase (en rouge), et
- un sinus avec un retard de phase (en vert).
y = A . cos(b . x + ε)
C'est l'équation générale d'une fonction sinusoïdale. Elle possède 3 paramètres : A, b et ε.
- A est appelé l'amplitude. La fonction oscillera entre les valeurs y = - A et y = + A.
- b affecte l'échelle horizontale. Quand b vaut 1(comme dans les exemples
ci-dessus), la fonction aura effectué un cycle après Δx = 2 . π rad.
Pour une autre valeur de b, le cycle sera Δx = 2 . π / b. - ε est appelé la constante de phase. C'est la valeur de la phase (c.à.d. de l'angle dont on calcule le cosinus) à x = 0. (voir exemples ci-dessus)
Lorsqu'on indique les valeurs de ces paramètres, on obtient une équation particulière.






