Courant continu

• prérequis
• courant
• loi d'Ohm
• générateur
• énergie, puissance
• résistances en série / parallèle
• mesures
• lois de Kirchhoff

Prérequis

• mathématiques : dérivées, intégrales
• dynamique : énergie
• électrostatique

courant électrique

= déplacement de charges, si circuit fermé (boucle)

sens du courant (convention) = sens de déplacement des charges +

intensité de courant I : "débit" de ce courant, charge / seconde; \( \class{formule}{ I = \dfrac{dq}{dt} }\)

unité : l'ampère (A)

Si j est la densité de courant, alors I = ∫ j • d£A

De façon plus générale, lorsque le courant résulte de différentes sortes de particules chargées,
j = ∑ n_i . q_i . v_i

Loi d'Ohm

Quand un courant traverse un conducteur, les charges perdent l'énergie ⇒ diminution du potentiel ⇒ U = Vavant - Vaprès U est appelé différence de potentiel. Ce U est proportionnel à I. cste de proportionalité : R ("résistance") ==> U = R . I On appelle aussi "résistance" ce conducteur lui-même. Unité de R : l'ohm (Ω).

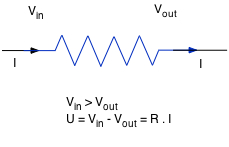Loi de Pouillet : \( \class{formule}{ R = \dfrac{ρ . L}{S} }\)

La résistivité ρ (qui est l'inverse de la conductivité σ) dépend de la température : ρ = ρ₀ . (1 + α . t)

De façon plus générale : \( \class{formule}{ \vec{j} = \dfrac{\vec{E}}{ρ} = σ . \vec{E} }\)

Générateur Pour donner de l'énergie aux charges, on utilise un générateur, qui fournit une différence de potentiel. En l'absence de courant, c'est la force électromotrice E ou f.e.m.. Les générateurs ont une résistance interne ri! générateur parfait : ri = 0

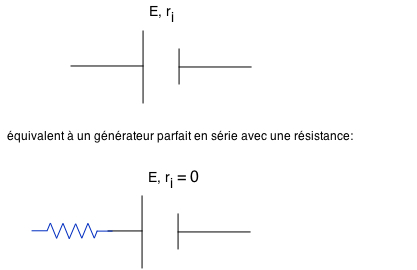Energie - puissance

Perte d'énergie dans une résistance : W = R . I² (transformée en chaleur, = effet Joule)

Puissance débitée par un générateur : P = E . I ⇒ énergie produite = E . I . t

Cette énergie produite par le générateur est entièrement utilisée par le circuit: chaleur, lumière (ampoules), mouvement (moteur)... ⇒ on peut appliquer la conservation de l'énergie.

Résistance en série / parallèle

Résistances en série

Les résistances sont placées les unes à la suite des autres, reliées uniquement par un fil sans noeud.
Elles sont toutes traversées par le même courant.

Cet ensemble de résistances équivaut à une seule résistance ( appelé résistance équivalente) dont la résistance vaut :

R = R₁ + R₂ + ...

Pour cette résistance équivalente, U = U_tot et I = I₁ = I₂ = ...

Résistances en parallèle

Les résistances ont leurs bornes supérieures sont reliées par un fil conducteur et leurs bornes inférieures sont reliées par un fil.
La différence de potentiel est la même aux bornes de chacun des éléments.

Cet ensemble de résistance équivaut à une seule résistance dont la résistance (la résistance équivalente) vaut :

\( \class{formule}{ R = (\dfrac{1}{R_1} + \dfrac{1}{R_2} + ... )^{-1} }\)

Pour cette résistance équivalente, I = I_tot et U = U₁ = U₂ = ...

Pour voir une méthode pour trouver les résistances en série et en parallèle, calculer la résistance équivalente, ainsi que leur courant et leur différence de potentiel dans un circuit contenant plusieurs résistances, cliquez ici.

Mesures

Mesure de U_AB

On branche un voltmètre entre A et B. (⇒ en parallèle sur le morceau de circuit entre A et B)
Voltmètre idéal : R = ∞

Mesure de I

On branche un ampèremètre en série dans la partie du circuit où circule le courant qu'on veut mesurer.
Ampèremètre idéal : R = 0
Pour les très faibles intensités de courant, il y a aussi le galvanomètre.

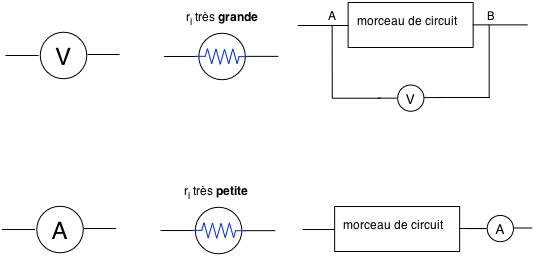
Mesure de R : on branche un ohmmètre aux bornes de la résistance, lorsque celle-ci est en dehors de tout circuit.

Lois de Kirchhoff

1. loi sur les intensités de courant

A chaque noeud, ∑ I_entrant = ∑ I_sortant

2. loi sur les différences de potentiel

Dans une maille, ∑U_i = 0
où U sont les diminutions (< 0) ou les augmentations (> 0) du potentiel rencontrées lorsqu'on parcourt toute la maille dans le même sens (arbitraire).