Les vecteurs
Prérequis
Définition
Un scalaire est un objet mathématique défini par
- un nombre et
- un signe.
Certaines grandeurs peuvent être décrites par des scalaires : le contenu de votre compte en banque, la masse, la charge électrique...
Un vecteur est un objet mathématique défini par
On le représente par une flèche.
Certaines grandeurs physiques peuvent être décrites par un vecteur : la position, la vitesse, une force, ...
Calcul des composantes
Soit le vecteur £C, qui fait un angle φ avec l'axe X.
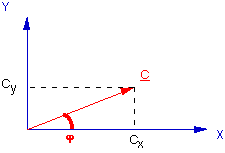
Le vecteur £C est la somme d'un vecteur £Cx dirigé selon l'axe X (projection orthogonale de £C sur X) et d'un vecteur £Cy dirigé selon l'axe Y (projection orthogonale de £C sur Y).
£Cx et £Cy sont les composantes vectorielles de £C.
La composante scalaire Cx (Cy) du vecteur £C est un scalaire,
- dont la valeur absolue est la norme du vecteur £Cx (£Cy),
- dont le signe est + si le vecteur £Cx (£Cy) est dans le même sens que l'axe X (Y), - s'il est de sens opposé à l'axe.
- Cx = signe . C . cosφ
- Cy = signe . C . sinφ
Attention : le sinus et le cosinus sont inversés si l'angle est donné par rapport à l'axe Y, donc ne pas apprendre ces formules par coeur mais faire à chaque fois un schéma clair et en déduire les composantes grâce à la trigonométrie.
Lorsque le vecteur £C est dirigé selon l'un des 2 axes,
- sa composante selon cet axe vaut (le signe) . (la norme de £C)
- l'autre composante est nulle.
Axe Z
Lorsqu'on travaille en 3 dimensions, il est nécessaire d'ajouter un troisième axe, Z, perpendiculaire au plan déterminé par X et Y.
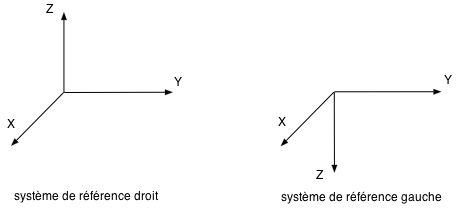
Pour le sens de cet axe, on choisira de préférence le sens "droit" : celui-ci est donné par le sens d'avancement d'un tire-bouchon qu'on fait tourner de façon à amener l'axe X vers l'axe Y par le côté le plus court. Le référentiel ainsi obtenu est appelé référentiel droit, ou droitier (le choix de l'autre sens donne un référentiel gauche, ou gaucher).
Notations
voir ici
Addition de vecteurs
La somme (encore appelée résultante ) de deux vecteurs £V1 et £V2 est un vecteur £R = £V1 + £V2 dont l'origine est l'origine de £V1 et l'extrémité est l'extrémité de £V2 lorsqu'on a translaté le second vecteur pour que son origine coincide avec l'extrémité du premier.

Pour faire la somme de vecteurs, on procède soit graphiquement, ou mieux, on calcule les composantes de chacun des vecteurs dans un système d'axes perpendiculaires X, Y et on applique les formules suivantes :
- Rx = V1x + V2x
- Ry = V1y + V2y
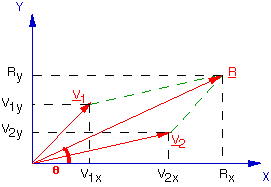
La norme de £R se calcule par \( \class{formule}{ R = \sqrt{(R_x^2 + R_y^2)} }\)
et l'angle qu'il fait avec l'axe X par \( \class{formule}{ θ = arctg \dfrac{R_y}{R_x} }\)
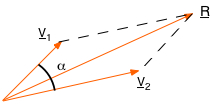
Si on veut juste trouver la norme de la résultante, on peut utiliser la formule \( \class{formule}{ R = \sqrt{(V_1^2 + V_2^2 + 2 . V_1 . V_2 . cosα)}}\) où α est l'angle entre les vecteurs £V1 et £V2 lorsqu'ils ont la même origine.
Multiplication de vecteurs
Il existe 2 types de multiplications de vecteurs entre eux :
On peut aussi multiplier un vecteur par un scalaire.Le produit scalaire
le résultat est un scalaire, positif ou négatif. Sa valeur se calcule par
c = a • b
⇒ c = a . b . cosθ où θ est l'angle entre les vecteurs a et b (voir ici pour d'autres méthodes de calcul)
Le produit vectoriel
le résultat est un vecteur dont la norme (c.à.d un scalaire positif) est donnée par
c = a Λ b ⇒ c = a . b . sinθ où θ est l'angle entre les vecteurs a et b (voir ici pour d'autres méthodes de calcul).
Orientation du vecteur c :
- direction perpendiculaire à a et à b (donc au plan défini par ces 2 vecteurs)
- sens : règle du tire-bouchon; lorsque les vecteurs ont même origine, on fait tourner le premier vecteur vers le second par le côté où c'est le plus court, et le sens de c est le sens dans lequel le tire-bouchon se déplace.
A ne pas confondre avec la
multiplication d'un vecteur par un scalaire
b = m . a où m est un scalaire
Le vecteur b a la même direction que a.
Son sens dépend du signe de m : si m est positif, alors b aura le même sens que a, alors que si m est négatif, alors b sera de sens opposé à celui de a.
Sa norme b = m . a






