Comment tracer p(t)

Voici une aide pour y parvenir. Libre à vous de la suivre, de l'adapter, de la simplifier.

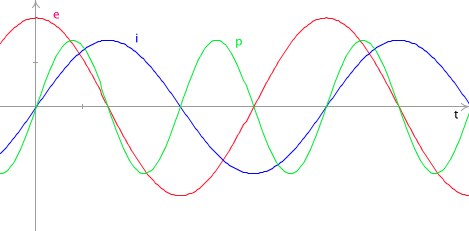
1. On connait: e(t) ou i(t) ⇒ représenter cette grandeur.
2. On calcule (par la représentation de Fresnel et la loi d'Ohm généralisée) le déphasage φ entre e et i ⇒ représenter l'autre grandeur, en décalant les 2 courbes de \( \class{formule}{ Δt = \dfrac{φ}{2π} . T }\)
3. On demande de tracer p(t).

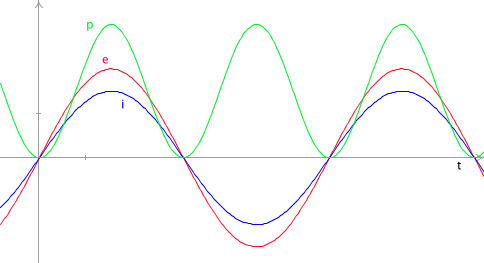
• à chaque temps où soit e soit i vaut 0, p vaut aussi 0,
• quand e et i sont de même signe, p est positif, quand ils sont de signes contraires, p est négatif,
• si à un t donné e et i sont plus grands qu'à un autre t, p sera aussi plus grand. On peut aussi remarquer (voir exemple 3 ci-dessous) qu'entre 2 zéros de p proches, p est plus petit qu'entre 2 zéros éloignés.
  

1. e et i en phase
   
2. i en retard de π/2 sur e
   
3. i en avance de π/4 sur e