Mouvements vibratoires
- prérequis
- mouvement oscillatoire harmonique : définitions, équations horaires et représentations
- théorème de Fourier
- cinématique et dynamique des mouvements oscillatoires harmoniques
- quelques cas particuliers (ressort, pendule simple, pendule de torsion)
- oscillations amorties
- oscillations forcées
Prérequis
- mathématiques :
- mécanique :
Oscillations harmoniques (vibrations)
Mouvement périodique : qui se reproduit identique à lui-même (1 cycle) pendant des intervalles de temps T successifs égaux.
\( \class{formule}{ \class{symbol}{f} = \dfrac{1}{T} }\) = fréquence (unité : 1 Hertz = 1 cycle / sec)
Cas particulier de mouvements périodiques : les mouvements oscillatoires harmoniques (MOH)
Ici, l'accélération varie sinusoïdalement. (c.à.d. que a n'est pas constante)
mouvement rectiligne : x = A . cos (ω . t + ε)
mouvement circulaire : θ = θm . cos (ω . t + ε)
où
A(θm) = amplitude = élongation maximum
ω, = pulsation = 2 . π . f
(ω . t + ε) = phase, parfois notée φ
ε = constante de phase (parfois notée φ, ou φ0 lorsque la phase est notée φ)
On peut aussi utiliser un sinus; dans ce cas, la constante de phase ε sera π/2 plus grande.
Représentation graphique
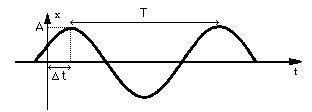
où \( \class{formule}{ Δt = - \dfrac{ε}{2π} . T }\)
Ici Δt > 0 (⇒ ε < 0), c.à. d. retard de phase.
Représentation vectorielle de Fresnel
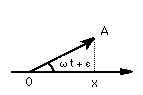
L'élongation x est la projection sur l'axe horizontal X d'un vecteur
- de longueur égale à l'amplitude,
- qui fait un angle avec l'axe horizontal égal à sa phase,
- et qui tourne dans le sens antihorlogique avec une vitesse angulaire égale à la pulsation.
(Si on utilise un sinus, x est la projection sur l'axe vertical).
Théorème de Fourier
Tout signal périodique peut se décomposer en une somme infinie de signaux harmoniques simples = développement en série de Fourrier :
\( \class{formule}{ S(t) = A_0 + \sum_{n=1}^∞ [A_n . cos(n . ω . t) + B_n . sin(n . ω . t)] }\) où ω est la pulsation de S(t).
Chaque terme est appelé harmonique.
En pratique, un nombre limité de termes suffit.
De la représentation S(t), on passe à une représentation A(n . ω) et B(n . ω).
Cinématique et dynamique des mouvements oscillatoires harmoniques
Ce qu'on a vu en cinématique et en dynamique reste valable, à savoir :
en cinématique
\( \class{formule}{ \vec{v} = \dfrac{\vec{dx}}{dt} }\)
\( \class{formule}{ \vec{a} = \dfrac{\vec{dv}}{dt} }\)
\( \class{formule}{ \vec{ω}_{(V.A.)} = \dfrac{\vec{dθ}}{dt} }\) , Vitesse Angulaire, à ne pas confondre avec la pulsation, aussi notée ω
\( \class{formule}{ \vec{α} = \dfrac{\vec{dω}_{(V.A.)}}{dt} }\)
(voir ICI une aide à la recherche de l'équation horaire)
en dynamique
∑ £F = m . a
∑ £M = I . £α
conservation de l'énergie totale (voir l'aide à la résolution de problèmes ICI)
Quelques cas particuliers de mouvements oscillatoires harmoniques
Le ressort
force de rappel : \( \class{formule}{ \vec{F} = - k . \vec{x} }\) ; k = cste de raideur
\( \class{formule}{ ω = \sqrt{\dfrac{k}{m}} }\)
\( \class{formule}{ E_{pot} = \dfrac{k . x^2}{2} }\)
Pour un ressort vertical, la position d'équilibre est simplement déplacée vers le bas de mg/k par rapport à un ressort horizontal.
Le pendule simple
moment de rappel : moment du poids
\( \class{formule}{ ω = \sqrt{\dfrac{g}{l}} }\)
Epot = énergie potentielle de pesanteur
Le pendule de torsion
moment de rappel : £M = - k . £θ ; k = coeff. de torsion
\( \class{formule}{ ω = \sqrt{\dfrac{k}{I}} }\)
\( \class{formule}{ E_{pot} = \dfrac{k . θ^2}{2} }\)
Le mouvement circulaire uniforme
Un mouvement circulaire uniforme est la composition de 2 mouvements harmoniques simples :
le long de 2 directions perpendiculaires
déphasés de π/2
de pulsation = vitesse angulaire
\( \class{formule}{ \vec{r} = R . cos(ω . t) . \vec{i} + R . sin(ω . t) . \vec{j} }\)
Oscillations propres amorties
= oscillations harmoniques + force de frottement visqueuse proportionnelle à v
Le ressort amorti :
Si £Frappel = - k . x et £Ffrott = - f . v ⇒ x = A . exp(- C . t) . sin(ω' . t + φ)
avec \( \class{formule}{ C = \dfrac{f}{2m} }\), \( \class{formule}{ ω' = \sqrt{ ω_0^2 - (\dfrac{f}{2m})^2} = \dfrac{1}{2m} . \sqrt{f^2 - 4 . m . k} }\) où \( \class{formule}{ \class{symbol}{ω_0} = \sqrt{\dfrac{k}{m} } }\) qui est la pulsation propre du ressort.
La forme de x(t) dépend de f2 - 4 . m . k :
|
|
Parfois, la constante de proportionnalité f de la force de frottement visqueuse est notée γ ou β, et est appelée coefficient d'amortissement.
Oscillations forcées
= oscillations harmoniques + force de frottement visqueuse + force extérieure harmonique
- £Frappel = - k . x
- £Ffrott = - f . v
- et £Fext = £Fm . cos(ω . t + ε)
⇒ l'oscillateur adopte un mouvement oscillatoire harmonique avec la pulsation de la force extérieure : v = vm cos(ω . t)
Le rapport \( \class{formule}{ \dfrac{F_m}{v_m} = \class{symbol}{Z} }\) se nomme impédance mécanique,
et la représentation graphique de Fresnel permet de voir que, dans le cas du ressort, dont la pulsation propre \( \class{formule}{ ω_0 = \sqrt{\dfrac{k}{m}} }\)
|
\( \class{formule}{ Z = \sqrt{f^2 + (m . ω - (\dfrac{k}{ω})^2} = \dfrac{m}{ω} . \sqrt{ (f . ω / m)^2+ (ω^2 - ω_0^2)^2 } }\) et \( \class{formule}{ tgε = \dfrac{(m . ω - k/ω)}{f} }\) vm devient maximum quand Z est minimum,
c.à.d. quand \( \class{formule}{ ω = ω_0 = \sqrt{ \dfrac{k}{m} } }\) , Pour l'élongation, x = A . sin(ω . t + φ), mais contrairement à des oscillations libres, A dépend de la fréquence : \( \class{formule}{ A = \dfrac{F_m/m}{\sqrt{(f . ω / m)^2+ (ω^2 - ω_0^2)^2 } }}\) |
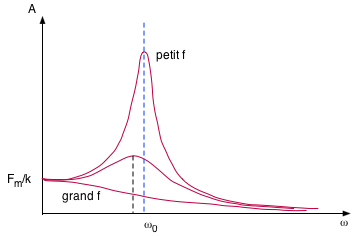 |