Dynamique - résolution de problèmes par la conservation de l'énergie
Voici une aide pour résoudre les problèmes de dynamique par la conservation de l'énergie. Libre à vous de suivre ces indications, de les adapter, de les simplifier (avec un peu d'habitude, vous ferez plusieurs de ces étapes mentalement).
Lors de la résolution d'un problème de dynamique, deux approches s'offrent à vous :
On peut bien sûr toujours choisir la méthode qu'on veut, sauf si l'énoncé en impose une. Mais comme pour tous les choix dans la résolution de problèmes de physique, on fera les choix qui mènent à des calculs les plus simples et les plus courts possible.
Donc en particulier, cela dépendra de ce qu'il faut calculer :
| v ---> conservation de l'énergie E ---> conservation de l'énergie |
a ---> seconde loi de Newton F ---> seconde loi de Newton |
Par la conservation de l'énergie :
Etot (t1) = Etot(t2)
Déterminer le système total (système isolé). Quels sont les différents corps qui le constituent ? Imaginons qu'il y en ait deux, A et B.
Choisir les instants t1 et t2 pour lesquels on va calculer l'énergie totale du système. Prendre pour un des instants celui pour lequel on doit calculer des grandeurs, et pour l'autre, un instant pour lequel on connait les grandeurs nécessaires au calcul de l'énergie totale.
Calculer les différentes formes d'énergie pour chacun des corps du système à l'instant t1.
Refaites la même chose pour l'instant t2.Pour chacun de ces deux instants séparément, additionner toutes les formes d'énergie de tous les corps du système : on obtient ainsi l'énergie totale du système :
- Etot(t1) = EtotA(t1) + EtotB(t1)
- Etot(t2) = EtotA(t2) + EtotB(t2)
- Appliquer la conservation de l'énergie, c.à.d. égaler ces deux expressions.
On peut éventuellement, dans un premier temps, s'aider d'un tableau :
| objets |
formes d'énergie |
à t1 |
à t2 |
|---|---|---|---|
| objet A |
EA1 EA2 ... -------------------------- EAtot = ∑ EAi |
||
| objet B |
EB1 EB2 ... -------------------------- EBtot = ∑ EBi |
||
| système |
Etot = EAtot + EBtot |
Note pour les mouvements qui associent translation et rotation d'un même corps.
Dans ce cas, il y a 2 formes d'énergie cinétique :
- de translation \( \class{formule}{ = \dfrac{m . V^2}{2} }\) où V est la vitesse du centre de masse du système
- de rotation \( \class{formule}{ = \dfrac{I . ω^2}{2} }\)
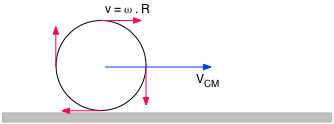
Dans la conservation de l'énergie, on remplace ω par son équivalent \( \class{formule}{ \dfrac{v}{R} }\), mais ATTENTION, ce v n'est pas le même que le V du centre de masse :
v est la norme de la vitesse des points extérieurs de l'objet, vitesse qui est tangente au cercle décrit par la rotation.
Cependant, on peut montrer que si l'objet roule sans glisser (grâce à la force de frottement statique), \( \class{formule}{ v = V }\).