Applications Didactiques de Physique

Cinématique

prérequis
description des mouvements
forme des équations horaires pour certains types de mouvements :
relation entre grandeurs linéaires et grandeurs angulaires
aide à la résolution de problèmes de cinématique

Prérequis

les mathématiques présentées sur ce site,
les généralités présentées sur ce site (alphabet grec, notations, arrondis, incertitudes, préfixes, ...).

Description d'un mouvement quelconque

On décrit le mouvement d'un point par le vecteur position, le vecteur vitesse et le vecteur accélération.

position : \( \class{formule}{ \class{symbol} { \vec{r} } }\)
vitesse : \( \class{formule}{ \class{symbol} { \vec{v} } = \dfrac{d\vec{r}}{dt} }\) , où le vecteur \( \vec{v} \) est toujours tangent à la trajectoire
accélération : \( \class{formule}{ \class{symbol} { \vec{a} } = \dfrac{d\vec{v}}{dt} }\)

La vitesse moyenne \( \class{formule}{ \class{symbol} { \vec{v}_m } = \dfrac{Δ\vec{r}}{Δt} }\)

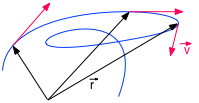La description du mouvement nécessite de connaitre l'équation horaire de ce mouvement, c.à.d. r = f(t).

Cette équation vectorielle r = f(t) se décompose en 3 équations scalaires, 1 selon chacune des 3 dimensions de l'espace (on choisit 3 axes perpendiculaires X, Y, Z) :

r_x = x = f_x(t)
r_y = y = f_y(t)
r_z = z = f_z(t)

Pour obtenir la vitesse,	Pour obtenir l'accélération,
\( \class{formule}{ v_x = \dfrac{dx}{dt} }\) \( \class{formule}{ v_y = \dfrac{dy}{dt} }\) \( \class{formule}{ v_z = \dfrac{dz}{dt} }\)	\( \class{formule}{ a_x = \dfrac{dv_x}{dt} }\) \( \class{formule}{ a_y = \dfrac{dv_y}{dt} }\) \( \class{formule}{ a_z = \dfrac{dv_z}{dt} }\)

Pour obtenir la vitesse,

Pour obtenir l'accélération,

\( \class{formule}{ v_x = \dfrac{dx}{dt} }\)

\( \class{formule}{ v_y = \dfrac{dy}{dt} }\)

\( \class{formule}{ v_z = \dfrac{dz}{dt} }\)

\( \class{formule}{ a_x = \dfrac{dv_x}{dt} }\)

\( \class{formule}{ a_y = \dfrac{dv_y}{dt} }\)

\( \class{formule}{ a_z = \dfrac{dv_z}{dt} }\)

Les équations de

x(t), y(t), z(t),
v_x(t), v_y(t), v_z(t),
a_x(t), a_y(t), a_z(t)

sont appelées équations du mouvement.

Cas particulier des mouvements rectilignes

Lors d'un mouvement rectiligne, il suffit d'avoir l'équation horaire (équation scalaire) selon l'axe qui est dans la direction de ce mouvement.
Dans beaucoup de cours de physique, on commence par étudier ce type de mouvement.

Cas particulier des mouvements dans un plan

Lorsque le mouvement se fait dans un plan, on prend alors 2 axes perpendiculaires X et Y dans ce plan.
On a alors 2 équations, l'une selon l'axe X et l'autre selon l'axe Y, comme si on avait 2 mouvements rectilignes concomitants.

On appelle ce mouvement, un mouvement composé, mais il s'agit donc simplement d'un mouvement général dans un plan, pour lequel on doit décomposer l'équation vectorielle du mouvement en 2 équations scalaires, chacune similaire à celle d'un mouvement rectiligne.

On indiquera parfois l'équation de la trajectoire y(x), que l'on trouve à partir de x(t) et y(t) en éliminant le temps.

Cas particulier des mouvements circulaires

Pour un mouvement circulaire dans un plan,

position : θ
vitesse angulaire : \( \class{formule}{ \class{symbol} { ω} = \dfrac{dθ}{dt} }\)
accélération angulaire : \( \class{formule}{ \class{symbol} { α} = \dfrac{dω}{dt} }\)

La vitesse angulaire moyenne \( \class{formule}{ \class{symbol} {ω_m} = \dfrac{Δθ}{Δt} }\)

Forme des équations horaires dans certains cas particuliers

Cas particulier où l'accélération est constante

Pour un mouvement dans un plan, avec axes X,Y :

équation vectorielle	équations des composantes (scalaires)
\( \class{formule}{ \vec{r} = \vec{r}_0 + \vec{v}_0~. t + \dfrac{\vec{a} . t^2}{2} }\)	\( \class{formule}{ x = x_0 + v_{0x}~. t + \dfrac{a_x~. t^2}{2} }\)
	\( \class{formule}{ y = y_0 + v_{0y}~. t + \dfrac{a_y~. t^2}{2} }\)
\( \class{formule}{ \vec{v} = \dfrac{d\vec{r}}{dt} = \vec{v}_0 + \vec{a} . t }\)	\( \class{formule}{ v_x = v_{0x} + a_x~. t }\)
	\( \class{formule}{ v_y = v_{0y} + a_y~. t }\)
\( \class{formule}{ \vec{a} = \dfrac{d\vec{v}}{dt} = \vec{cste} }\)	\( \class{formule}{ a_x = cste_{x} }\)
	\( \class{formule}{ a_y = cste_{y} }\)

Mouvements circulaires avec accélération angulaire constante

\( \class{formule}{ θ = θ_0 + ω_0~. t + \dfrac{α . t^2}{2} }\)

\( \class{formule}{ ω = \dfrac{dθ}{dt} = ω_0 + α . t }\)

\( \class{formule}{ α = \dfrac{dω}{dt} = cste }\)

Mouvements oscillatoires harmonique

Voir cette page.

Relations entre grandeurs linéaires et grandeurs angulaires: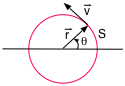

grandeur	direction et sens
S = θ . r
v = ω . r	tangent au cercle, dans le sens du mouvement
a_c = ω² . r	radial, vers le centre du cercle
a_t = α . r	tangent au cercle, dans le sens du mouvement si accélération, et opposé au mouvement si décélération

\( \class{formule}{ \vec{a} = \vec{a}_c + \vec{a}_t }\)

L'accélération tangentielle \( \class{formule}{ \class{symbol}{\vec{a}_t} }\) représente la variation de la grandeur du vecteur vitesse.
L'accélération centripète \( \class{formule}{ \class{symbol}{\vec{a}_c} }\) représente la variation de la direction du vecteur vitesse.

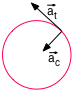C'est la décomposition du vecteur accélération selon 2 axes perpendiculaires : l'un tangent à la trajectoire, l'autre perpendiculaire à la trajectoire.

Correspondance entre grandeurs linéaires et grandeurs angulaires

r -------> θ
v -------> ω
a -------> α

Aide à la résolution de problèmes de cinématique