Acoustique
Prérequis
- mécanique : hydrostatique (notion de pression),
- phénomènes vibratoires :
Nature
1) pression acoustique
onde de compression (allez voir l'animation)
p = dP = pression acoustique = variation de pression
\( \class{formule}{ p = \dfrac{2πA}{k.λ} . cos [2π . (\dfrac{t}{T} - \dfrac{y}{λ})] }\) (A = amplitude de la vibration des molécules, k = coefficient de compressibilité )
La pression acoustique est proportionnelle à la vitesse de vibration des molécules; la constante de proportionnalité Z est appelée impédance acoustique : p = Z . v
2) intensité acoustique
I = p . v = intensité acoustique = puissance acoustique transmise par unité de surface
I est proportionnelle à \( \class{formule}{ \dfrac{1}{S} }\) (surface du front d'onde), et au carré de la pression acoustique : \( \class{formule}{ I = \dfrac{p^2}{Z} }\)
Dépendance à la distance à la source (r) : \( \class{formule}{ I ∝ \dfrac{1}{S} }\) ⇒
| onde sphérique | \( \class{formule}{ \dfrac{1}{r^2} }\) |
| onde circulaire |
\( \class{formule}{ \dfrac{1}{r} }\) |
| onde plane |
cste |
3) Célérité
- Dans un solide : \( \class{formule}{ c = \sqrt{\dfrac{E}{ρ}} }\) où E = module d'élasticité, et ρ = masse volumique du solide
- Dans un liquide : \( \class{formule}{ c = \sqrt{\dfrac{B}{ρ}} }\), où B est le module d'élasticité volumique
- Dans un gaz : \( \class{formule}{ c = \sqrt{ \dfrac{1}{k . ρ}} = \sqrt{\dfrac{γ. P}{ρ}} = \sqrt{\dfrac{γ . R . T }{ M}} }\) où k = coefficient de compressibilité et M la masse molaire du gaz
Z = c . ρ
Dans l'air à 15 °C, c = 340 m/s et Z = 400 kg /(m . s)
Production
cordes, tuyaux : ondes stationnaires
f2 = 2 . f1, f3 = 3 . f1, ... = les harmoniques
Calcul de ces fréquences :
- trouver les longueurs d'onde possibles (par un petit dessin, voir la fondamentale et f2 pour une corde
 , un tuyau ouvert
, un tuyau ouvert  et un tuyau fermé
et un tuyau fermé  )
) - calculer la fréquence correspondante par \( \class{formule}{ f = \dfrac{c}{λ} }\)
Tuyau fermé : uniquement les harmoniques impaires
Extrémité libre (corde) ou ouverte (tuyau) = ventre
Extrémité fixe (corde) ou fermée (tuyau) = noeud
corde : \( \class{formule}{ c = \sqrt{\dfrac{T}{m}} }\) où T = tension,
m = masse par unité de longueur (!)
tuyau : \( \class{formule}{ c = \sqrt{\dfrac{1}{kρ}} }\) où k = coeff. de compressibilité, ρ = masse vol.
Effet Doppler
Lorsque l'observateur ou la source de l'onde se déplacent, la fréquence perçue est modifiée.
- observateur mobile (v), source fixe
 ⇒ \( \class{formule}{ c' = c ± v }\) ⇒ \( \class{formule}{ f'= \dfrac{c'}{λ} }\)
⇒ \( \class{formule}{ c' = c ± v }\) ⇒ \( \class{formule}{ f'= \dfrac{c'}{λ} }\) - observateur fixe, source mobile (v)
 ⇒ \( \class{formule}{ λ' = λ ± v.T }\) ⇒ \( \class{formule}{ f'= \dfrac{c}{λ'} }\)
⇒ \( \class{formule}{ λ' = λ ± v.T }\) ⇒ \( \class{formule}{ f'= \dfrac{c}{λ'} }\)
Plus de détails ici.
Propagation
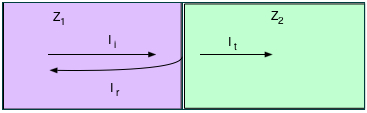
Lors d'un changement de milieu, il y a réflexion et transmission.
| coeff. de réflexion \( \class{formule}{ \class{symbol}{r} = \dfrac{I_r}{I_i} }\) coeff. de transmission \( \class{formule}{ \class{symbol}{t} = \dfrac{I_t}{I_i} }\) |
et r + t = 1 quand on peut négliger l'absorption. |
La fréquence ne change pas.
|
\( \class{formule}{ r = [\dfrac{(Z_2 - Z_1)}{(Z_2 + Z_1)}]^2 }\) \( \class{formule}{ t = \dfrac{4 Z_1 . Z_2}{(Z_2 + Z_1)^2} }\) |
 |
On peut aussi calculer l'affaiblissement en décibels : 10 . log t






