Dynamique - Hydrostatique

Hydrostatique : v = 0

• prérequis
• 2 nouvelles forces et concept de pression
  
• conséquences de ces forces :
  • conséquences de la pression : force d'Archimède, énergie de pression
  • conséquences des forces de cohésion et d'adésion : tension superficielle
• 2 types de problèmes : étude d'un objet dans un fluide / étude du fluide dans son récipient
  

Prérequis

• la dynamique du point,
• l'énergie.

Deux nouvelles forces

1. Force de pression £F (normale aux surfaces), due aux chocs des particules du fluide sur la surface. Les molécules du fluide ont des mouvements désordonnés, ce qui engendre des chocs sur les surfaces des objets plongés dans le fluide. A chaque choc, il y a changement de la quantité de mouvement de la molécule, et donc une force est exercée sur la surface.

   Si on change l'orientation de la surface sur laquelle s'exerce cette force, on obtient toujours une force de même norme, ce qui conduit à utiliser une autre modélisation, et on définit plutôt une nouvelle grandeur scalaire (donc sans orientation) :

   la pression : \( \class{formule}{ \class{symbol}{P} = \dfrac{F}{S} }\) ,
   

   où F est la norme de la force qui s'exercerait sur la surface S d'un objet si on plaçait cet objet à cet endroit, mais il n'est pas nécessaire qu'il y ait un objet dans le fluide pour y calculer une pression.

   On peut aussi définir la pression comme le travail exercé par cette force lorsqu'elle déplace la surface sur laquelle elle s'exerce : \( \class{formule}{ P = \dfrac{dW}{dV} }\)
   dV est la variation de volume qui résulte de ce déplacement.
   Il est d'ailleurs souvent plus facile de penser à la pression comme une énergie par unité de volume que comme la norme d'une force par unité de surface.
   

   unité :

   SI : le Pascal (Pa)

   l'atmosphère, 1 atm = 101 300 Pa

   (voir ici pour les autres unités)

   
   

2. Forces de cohésion et d'adhésion

   = force entre les molécules du liquide (cohésion) et entre les molécules du liquide et celles de son récipient (adhésion)
   

   
   

    

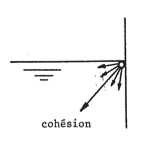
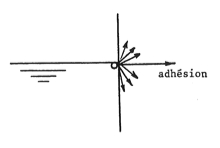
Conséquences des forces de pression

1. La force d'Archimède, résultante des forces de pression sur les parois d'un objet. Elle est verticale vers le haut, et FA = ρ . g . V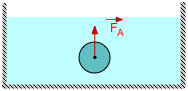

2. Une nouvelle forme d'énergie : l'énergie de pression, qui est l'énergie mécanique interne du fluide.
   

   Conservation de l'énergie ⇒ E_press + m . g . h = cste (dans l'espace !) (v = 0)

   On l'utilise plutôt sous la forme : \( \class{formule}{ \dfrac{E_{press}}{V} + ρ . g . h = cste }\)

   • \( \class{formule}{ \dfrac{E_{press}}{V} }\) se note p et est appelée pression hydrostatique (ou juste pression). Pour un gaz, cette énergie est l'énergie cinétique des particules de ce gaz (agitation thermique).
   • Le terme ρ . g . h , qui est l'énergie potentielle d'une unité de volume, est appelé la pression de pesanteur ou pression de gravitation.
     
   • La somme de ces 2 termes, qui est l'énergie totale dans une unité de volume, est appelée pression totale.

   Attention : seule la pression hydrostatique est une vraie pression, dans le sens où seulement celle-là donne lieu à une force sur une surface.
   Les autres termes dits de "pression" ont seulement les dimensions d'une pression.
   

   On a donc p + ρ . g . h = cste

   ⇒	En deux points situés à une même hauteur par rapport au fond, si on a le même liquide, on aura la même pression hydrostatique. Si on descend d'une profondeur x dans un liquide de masse volumique ρ, on a une augmentation de la pression hydrostatique : Δp = ρ . g . x

   
   

Conséquences des forces de cohésion et d'adhésion

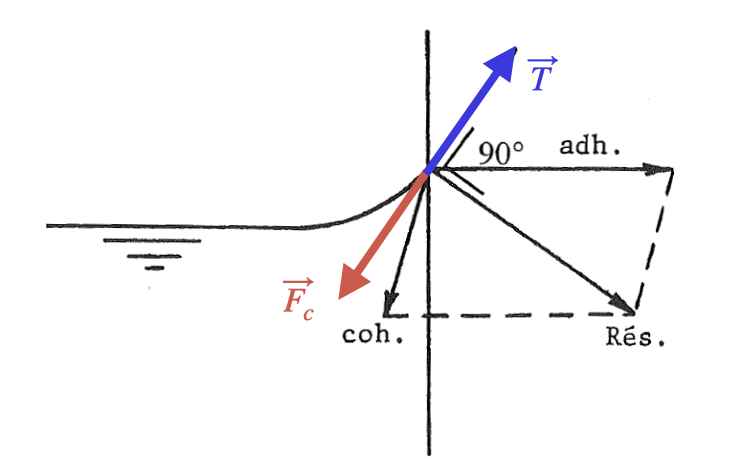
Le liquide monte (ou descend) le long de la paroi du récipient COMME SI il y avait une force T qui tirait sur la surface. Dans ce modèle, cette force est proportionnelle à la longueur de contact avec le récipient, et la constante de proportionnalité, c'est la tension superficielle : \( \class{formule}{ \class{symbol}{f} = \dfrac{T}{l} }\). Vu autrement, la surface du liquide se comporte un peu comme un ballon de baudruche, exerçant une force, la force capillaire Fc, sur la paroi du récipient. Cette force est tangente à la surface du liquide et tend à minimiser celle-ci. Dans ce modèle, on a \( \class{formule}{ \class{symbol}{f} = \dfrac{F_c}{l} }\) On préfère souvent une autre définition: \( \class{formule}{ f = \dfrac{dW}{dS} }\) travail par unité de surface qu'il faut fournir pour agrandir la surface. unité SI : N/m ou J/m2

Capillaires : différence de niveau de liquide avec l'extérieur du capillaire de \( \class{formule}{ h = \dfrac{2 . f . cosα}{ρ . r . g} }\) (loi de Jurin)

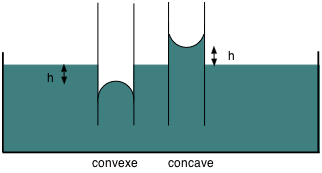
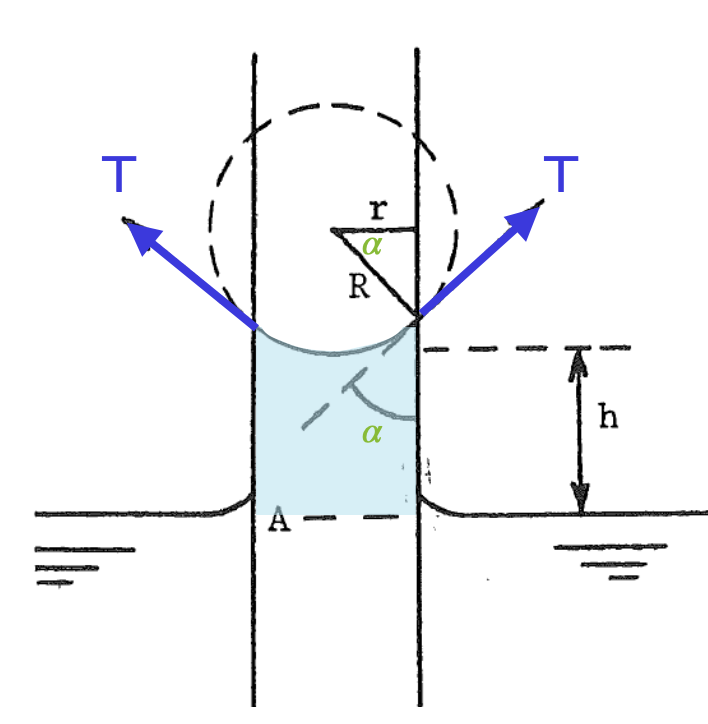
Variation de pression à la surface d'un liquide : si surface plane, \( \class{formule}{ P(in) = P(out) }\) si surface convexe, \( \class{formule}{ P(in) = P(out) + \dfrac{2 . f}{R} }\) si surface concave, \( \class{formule}{ P(in) = P(out) - \dfrac{2 . f}{R} }\) Dans les 2 derniers cas, on a \( \class{formule}{ P(côté~concave) - P(côté~convexe) = \dfrac{2 . f}{R} }\) (loi de Laplace) où R est le rayon de courbure de la surface.

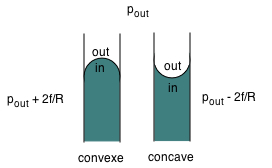2 types de problèmes

1. On étudie un objet dans un fluide ⇒ ∑£F = m . a , avec force d'Archimède

2. On étudie le fluide dans son récipient ⇒ p + ρ . g . h = cste ou ses conséquences, et tension superficielle.
   Pour un exemple de méthode de résolution de problème de calcul de pressions, voir ici.