Ondes progressives
Prérequis
- mathématiques : trigonométrie,
- phénomènes vibratoires : mouvements oscillatoires harmoniques.
Définitions
Soit une source ayant un mouvement vibratoire (MOH): x = A . cos(ω . t + ε0).
L'onde progressive est la propagation de proche en proche de ce mouvement vibratoire à une vitesse c, appelée célérité.
On peut aussi la concevoir comme une succession infinie d'impulsions de forme sinusoïdale.
⇒ retard Δt qui dépend de la distance à la source y : \( \class{formule}{ Δt = \dfrac{y}{c} }\)
⇒ à cet endroit, \( \class{formule}{ x = A . cos(ω . (t - Δt) + ε_0) = A . cos[2π . ( \dfrac{t}{T} - \dfrac{y}{λ}) + ε_0] }\)
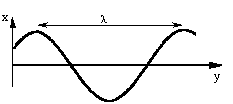
où λ = longueur d'onde = distance entre 2 maxima successifs = c . T
Deux représentations graphiques possible
Pour t fixé : |
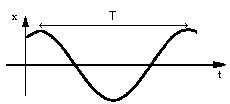
Pour y fixé : |
|---|---|
|
|