γ (gamma)
Les rayons γ ou photon γ, ou plus simplements les γ sont des ondes électromagnétiques de grande énergie (et donc de petite longueur d'onde), nommées ainsi lorsqu'elles sont produites par le noyau atomique dans les transformations radioactives ou les réactions nucléaires).
galvanomètre
Un galvanomètre est un appareil qui sert à mesurer des intensités de courant faibles.
gamma-caméra
Une gamma-caméra est le détecteur utilisé en scintigraphie pour détecter les rayons gammas issus des radioisotopes se trouvant dans le corps.
Gauss (théorème - surface - distribution - unité)
Johann Carl Friedrich Gauss est un physicien-mathématicien allemand (1777 - 1855).
1- En électrostatique
théorème de Gauss : le flux du champ électrique à travers une surface fermée (appelée surface de Gauss) est égal au rapport entre la charge électrique contenue à l'intérieur de cette surface et la permittivité du milieu.
2- En statistiques, on utilise aussi la loi normale de Gauss ou la distribution gaussienne ou tout simplement gaussienne pour désigner la façon dont se répartissent les résultats d'un grand nombre de mesures d'une même grandeur physique sous l'influence d'un grand nombre de facteurs agissant séparément de façon additive, certains positivement, d'autres négativement, sans qu'il y ait prépondérance marquée de l'un ou de l'autre de ces facteurs.
Elle est donnée par la fonction mathématique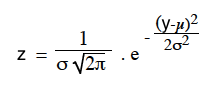 
qui, graphiquement est en forme de cloche, et où
- y est la grandeur qu'on mesure,
- z est le nombre de fois qu'une valeur particulière de y apparait,
- μ est la valeur centrale de la cloche (valeur la plus probable), et
- σ (appelé la déviation standard) donne l'étalement de cette cloche.
La probabilité qu'une mesure de y tombe dans l'intervalle [μ - σ ; μ + σ] , calculée en intégrant de z de μ - σ à μ + σ, est de 68%.
3- C'est aussi une unité de champ magnétique (voir ce terme).
gaz
Un gaz est un matériau qui n'a ni volume ni forme propre. Celles-ci dépendent du conteneur dans lequel il se trouve, et dont il occupe tout le volume, ceci en raison des forces de liaison extrêmement faibles entre ses constituants (molécules ou atomes).
gaz monoatomique
Un gaz monoatomique est un gaz dont les molécules sont constituées d'un seul atome. Ce sont les atomes d'hélium, de néon, d'argon, ... On les appelle aussi gaz inertes ou gaz rares.
A distinguer des gaz diatomiques, dont les molécules sont constituées de 2 atomes, soit de même type (molécules homonucléaires) soit de types différents (molécules hétéronucléaires).
gaz parfait
Un gaz parfait est un gaz satisfaisant à 3 hypothèses :
- le volume des molécules est négligeable, on peut les considérer comme des points géométriques,
- les molécules sont indépendantes les unes des autres, elles n'exercent aucune interaction à distance,
- les chocs sont parfaitement élastiques.
Les gaz qu'on rencontre dans la pratique, et qui ne satisfont pas tout à fait ces conditions, sont appelés gaz réels.
générateur
Un générateur, ou source de courant, ou source de tension, est un appareil qui crée une différence de potentiel entre ses deux bornes.
On appelle pôle positif ou borne positive, la borne au potentiel le plus élevé, et pôle négatif ou borne négative, la borne au potentiel le plus bas.
Il existe différents types de générateurs :
La pile, où l'énergie électrique est produite à partir d'énergie chimique.
L'alternateur, où l'énergie électrique est produite à partir d'énergie mécanique. L'alternateur produit une tension alternative par rotation d'un groupe de spires dans un champ magnétique. Il est constitué de l'inducteur (ce qui produit un champ magnétique) et de l'induit (les spires qui sont le siège de la force électromotrice induite).
Le générateur de tension continue, basé sur le même principe que l'alternateur, mais où la connexion des spires au circuit extérieur est différente. Il produit une différence de potentiel continue.
La photo-pile, où l'énergie électrique est produite à partir d'énergie lumineuse.
L'alimentation électrique, où l'énergie électrique est produite à partir d'énergie électrique.
générateur parfait :
Un générateur parfait est un générateur qui crée toujours la même différence de potentiel E (ou E), appelée force électromotrice, entre ses deux bornes, quel que soit le courant qui le traverse.
résistance interne :
Dans la réalité, la différence de potentiel aux bornes du générateur est d'autant plus faible que le courant est grand car il y a des conducteurs dans le générateur dont la résistance n'est pas nulle. La résistance interne ri est la résistance de l'ensemble de ces conducteurs. Un générateur réel peut donc être représenté comme un générateur parfait en série avec une résistance : la résistance interne.
gradient
Le gradient d'une fonction scalaire f de x, y et z est un vecteur dont les composantes selon les 3 axes de coordonnées sont les dérivées partielles de f par rapport à x, y et z. Il indique comment varie la fonction lorsqu'on se déplace selon chacune des 3 directions de l'espace.
Il est perpendiculaire aux courbes de niveau (courbes où f est constante) et donne la direction de la plus grande pente (dans la zone où les courbes se resserrent).
Parfois, on appelle "gradient d'une grandeur V" une grandeur V qui varie régulièrement le long d'une direction de l'espace.
gradient de concentration
Le gradient de concentration est un nombre qu'on calcule en faisant le rapport entre la variation de concentration entre deux points et la distance entre ces points : grad c = Δc/Δx
gramme
Voir "masse"
gramme-force, gramme-poids
Voir "poids"
grand axe
Voir "ellipse"
grandeur de base
grandeur dérivée
Une grandeur dérivée est une grandeur physique qui est définie à partir d'autres grandeurs qui sont déjà connues.
exemple : la vitesse
Contraire de grandeur fondamentale.
grandeur fondamentale
Une grandeur fondamentale ou grandeur de base est une grandeur physique qui n'est pas définie à partir d'autres grandeurs.
exemples : la distance, le temps.
Contraire de grandeur dérivée.
grandeur mesurable
Une grandeur mesurable est une grandeur physique que l'on peut exprimer comme un multiple d'une valeur de référence de cette grandeur.
exemple : une longueur est le double, le triple... d'une longueur de référence.
contre-exemple : la température, qu'on repère seulement sur une échelle.
grandeur physique
Une grandeur physique est une propriété de la nature que l'on peut représenter par un scalaire (grandeur scalaire) ou par un vecteur (grandeur vectorielle, dont la norme est un scalaire).
grandeur supplémentaire
Une grandeur supplémentaire est une grandeur physique pour laquelle on n'a pas décidé s'il s'agit d'une grandeur fondamentale ou d'une grandeur dérivée.
exemples : les angles plans et angles solides.
grandeur vectorielle
Voir "grandeur physique"
grandissement
Le grandissement transversal, ou plus simplement grandissement, G (attention, même notation que pour le grossissement), en optique, est le rapport entre la taille de l'image (I) et la taille de l'objet (O) (image d'un objet obtenue par réflexion sur un miroir ou réfraction à travers une lentille) : G = I/O
Il peut y avoir une autre notation (m ou g) et une autre définition : m = yI / yO où yI et yO correspondent à I et O mais avec un signe : positif si au-dessus de l'axe optique, négatif en-dessous.
On utilise généralement le grandissement quand on a une image réelle.
Pour une image virtuelle, on utilise plutôt le grossissement.
unité : sans
graphe semi-logarithmique
Voir "papier semi-logarithmique"
gravitation
gray
Voir "dose"
grossissement
Le grossissement angulaire, ou plus simplement grossisement, G (attention, même notation que pour le grandissement) en optique, est le rapport entre le diamètre apparent de l'image et le diamètre apparent de l'objet (image d'un objet obtenue par réflexion sur un miroir ou réfraction à travers une lentille) : G = tgθI / tgθO
Le grossissement d'un microscope est le produit du grandissement de son objectif par le grossissement commercial de son oculaire.
On utilise généralement le grossissement lorsqu'on a une image virtuelle.
Pour une image réelle, on utilise plutôt le grandissement.
unité : sans
grossissement commercial
Le grossissement commercial (G ou Gcomm ou G∞), en optique, est le grossissement calculé dans des conditions précises : c'est le rapport entre le diamètre apparent de l'image quand l'oeil est placé au foyer de la lentille ou du miroir, et le diamètre apparent de l'objet quand l'oeil est placé à la distance minimale de vision nette normale : 25 cm.
Pour une loupe, on peut montrer qu'alors G = 25 / f où f est la distance focale exprimée en cm.
unité : sans