Primitives et intégrales
Prérequis
Primitives et intégrales indéfinies
Trouver la primitive d'une fonction est l'inverse de l'opération qui consiste à trouver la différentielle d'une fonction. C.à.d. qu'on cherche la fonction dont dy est la différentielle.
| différentier | ||
| Soit y = y(x) | =========> | dy = y' . dx = f(x) . dx |
| primitiver | ||
| y(x) = ∫ dy | <======= | dy = f(x) . dx |
Comme toutes les fonctions qui ne diffèrent que d'une constante ont la même dérivée y' (puisque la dérivée d'une constante est nulle) et donc la même différentielle dy, on doit rajouter une constante arbitraire, appelée constante d'intégration, au résultat de la primitivation pour obtenir l'ensemble de toutes les primitives : ∫ dy = ∫ f(x) . dx = y(x) + C = F(x)
L'ensemble de toutes les primitives est appelé l'intégrale indéfinie.
Et pratiquement, vous devrez donc trouver de quelle fonction f(x) est la dérivée.
Vous pouvez vous aider des formules que vous trouverez dans la section formules.
Vérification : lorsque vous avez calculé une primitive F(x) de la différentielle d'une fonction dy = f(x) . dx, nous vous conseillons vivement de vérifier votre résultat en le dérivant : F '(x) = f(x)
Intégrales définies
C'est la différence entre la primitive F en un point d'abscisse x = b et un autre point d'abscisse x = a :
∫ab f(x) . dx = F(b) - F(a).
a et b sont appelées les bornes d'intégration.
On peut montrer qu'elle représente l'aire de la surface comprise entre la courbe de f(x) au-dessus, l'axe des x en-dessous, et les droites verticales x = a et x = b.
Dans l'exemple ci-dessous, l'intégrale définie de la fonction f(x) entre a et b vaut l'aire de la surface bleu clair.
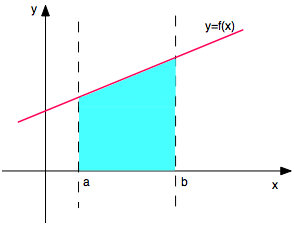
Calculer l'intégrale définie équivaut à faire une somme d'un très grand nombre de termes f(xi) . Δx avec xi qui sont les valeurs centrales des intervalles de largeur Δx et qui vont de a à b, lorsque la largeur Δx tend vers zéro.
Application de l'intégrale définie : calcul de la moyenne d'une fonction f(x) sur un intervalle [a,b] :
\( \class{formule}{\overline{f} = \dfrac{\int_{a}^{b} f(x) . dx}{(b - a)}} \)
Voir quelques propriétés des intégrales définies dans la section formules.






