Circuits avec R, L et C
- prérequis
- le problème
- équations différentielles
- solutions pour RL
- solutions pour RC (charge et décharge du condensateur)
- solution LC
- solutions RLC
Prérequis
- Mathématiques : exponentielles, sinusoïdes, dérivées, équations différentielles,
- Electricité : électrostatique, courant continu, induction
Le problème
On a un circuit avec des combinaisons des éléments suivant : R, L et C.
Le générateur fournit une force électro-motrice variable dans le temps, par créneaux.
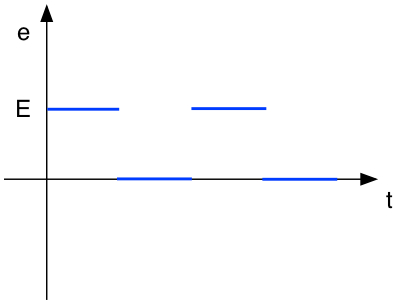 OU
OU 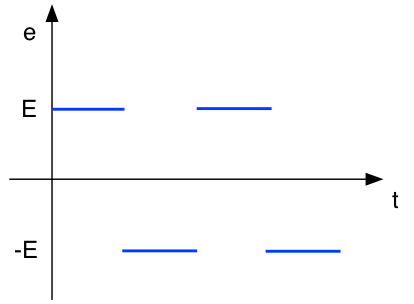
On cherche l'intensité du courant, la différence de potentiel aux bornes des différents éléments, et, s'il y a un condensateur, sa charge, en fonction du temps.
Equations différentielles
En appliquant les lois de Kirchhoff (ou la loi d'Ohm généralisée) à un circuit avec générateur, R, L et C, on obtient des équations différentielles avec comme variables, selon les cas, e(t), i(t), q(t) et leur dérivée par rapport à t.
| Kirchhoff ou loi d'Ohm généralisée |
⇒ | équation différentielle |
RL
solutions avec les fonctions
- \( \class{formule}{ exp(\dfrac{-t}{τ}) }\) (fonction décroissante), ou
- \( \class{formule}{ 1 - exp(\dfrac{-t}{τ}) }\) (fonction croissante)
τ est appelée la constante de temps.
Après un temps t = τ, l'exponentielle est égale à 0,37 fois sa valeur à t = 0.
RL: \( \class{formule}{ τ = \dfrac{L}{R} }\)
Pour trouver la forme exacte de eR(t), eL(t), i(t), se demander, pour chacune des 2 demi-périodes du générateur, si la fonction qu'on cherche est croissante ou décroissante.
Il ne reste plus alors qu'à calculer
- la constante de temps τ
- par quelle constante on doit multiplier la fonction \( \class{formule}{ exp(\dfrac{-t}{τ}) }\) (si grandeur décroissante), ou la fonction \( \class{formule}{ 1 - exp(\dfrac{-t}{τ}) }\) (si grandeur croissante).
RC (charge et décharge du condensateur)
solutions avec fonctions
- \( \class{formule}{ exp(\dfrac{-t}{τ}) }\) (fonction décroissante), ou
- \( \class{formule}{ 1 - exp(\dfrac{-t}{τ}) }\) (fonction croissante)
τ est appelée la constante de temps.
Après un temps t = τ, l'exponentielle est égale à 0,37 fois sa valeur à t = 0.
RC : τ = RC
Pour trouver la forme exacte de eR(t), eC(t), i(t), q(t), se demander, pour chacune des 2 demi-périodes du générateur, si la fonction qu'on cherche est croissante ou décroissante.
Il ne reste plus alors qu'à calculer :
- la constante de temps τ
- par quelle constante on doit multiplier la fonction \( \class{formule}{ exp(\dfrac{-t}{τ}) }\) (si grandeur décroissante), ou la fonction \( \class{formule}{ 1 - exp(\dfrac{-t}{τ}) }\) (si grandeur croissante).
LC
circuit oscillant i = Im . cos(ω . t + φ), avec \( \class{formule}{ ω = \dfrac{1}{\sqrt{LC}} }\)
L'énergie passe alternativement du condensateur à la self et inversement.
RLC
|
oscillations sinusoïdales amorties si \( \class{formule}{ R^2 - 4 \dfrac{L}{C} < 0 }\) oscillations critiques si \( \class{formule}{ R^2 - 4 \dfrac{L}{C} = 0 }\) oscillations apériodiques si \( \class{formule}{ R^2 - 4 \dfrac{L}{C} > 0 }\) |
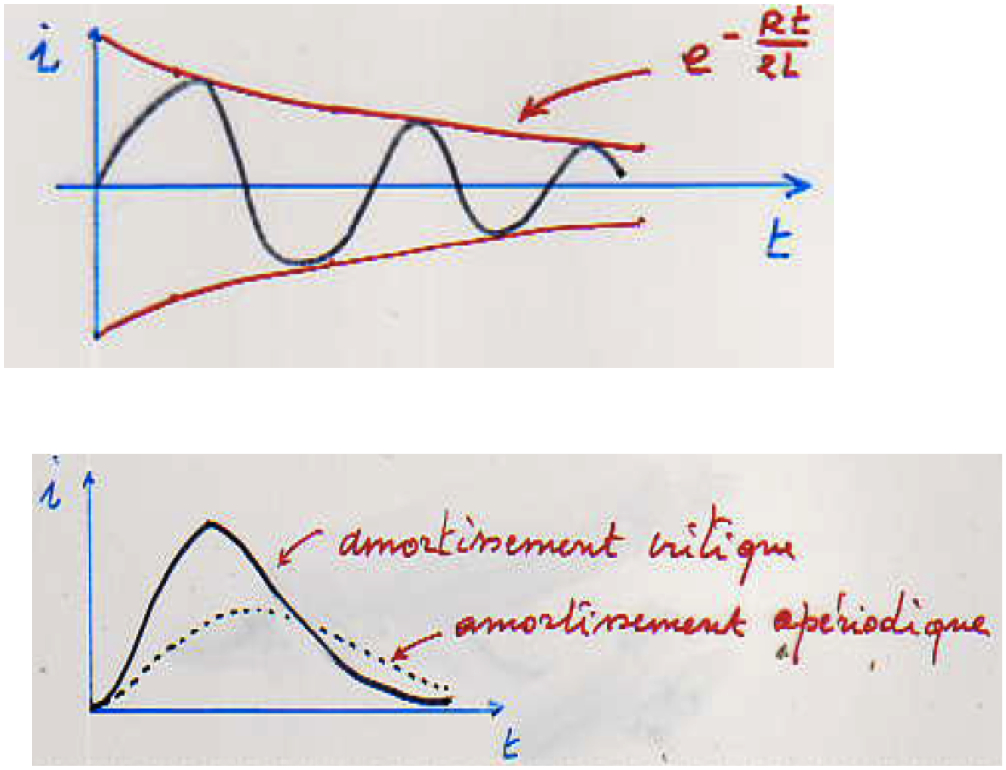 |






