Fonctions - les exponentielles
- prérequis
- la fonction exponentielle : définition
- y = a . exp(b . x)
- y = a . exp(-b . x)
- y = a . (1 - exp(-b . x))
Prérequis
La fonction exponentielle : définition
La fonction exponentielle est la fonction y = f(x), notée exp(x) telle que exp(x) = ex
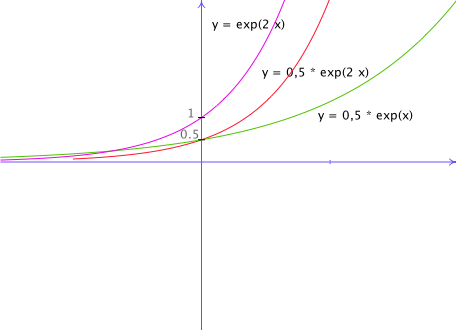
y = a . exp( b . x) avec b > 0
a et b sont les paramètres de cette fonction.
L'équation y = a . exp( b . x) est l'équation générale d'une exponentielle croissante.
En remplaçant les lettres a et b (les paramètres) par des valeurs, selon ces valeurs, on obtient différentes exponentielles (= équations particulières).
- a est la valeur de l'ordonnée à l'origine.
- a . b est la pente de la tangente à la courbe en x = 0. Cette droite coupe l'axe X en x = -1/b.
Pour un même a, b indique donc la rapidité de la croissance de la fonction.
Plus utilisée en physique :
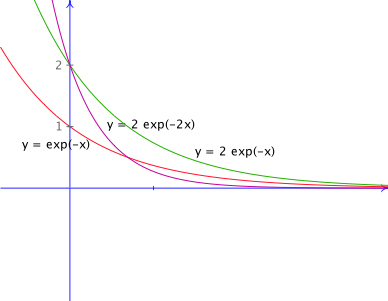
y = a . exp(-b . x) avec b > 0
a et b sont les paramètres de cette fonction. L'équation y = a . exp( -b . x) est l'équation générale d'une exponentielle décroissante.
En remplaçant les lettres a et b (les paramètres) par des valeurs, selon ces valeurs, on obtient différentes exponentielles décroissantes (= équations particulières).
- a est la valeur de l'ordonnée à l'origine.
- - a . b est la pente de la tangente à la courbe en x = 0. Cette droite coupe l'axe X en x = 1/b.
Pour un même a, b indique donc la rapidité de la décroissance de la fonction.
On peut trouver la valeur de 1/b en traçant la tangente à l'origine. Celle-ci coupe l'axe des abscisses à x = 1/b.
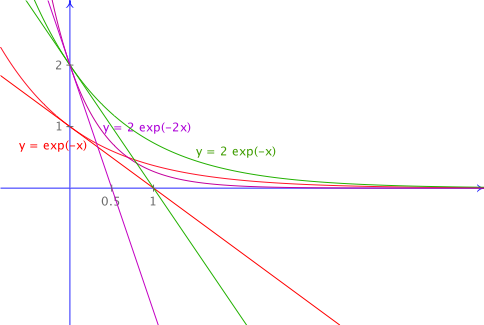
La valeur de 1/b est la valeur de x pour laquelle la grandeur y ne vaut plus que 0.37 fois sa valeur initiale.
Quand x est le temps, alors 1/b est la constante de temps; c'est le temps au bout duquel la grandeur y ne vaut plus que 0.37 fois sa valeur initiale.
Tout autant utilisée :
y = a . (1 - exp(-b . x))
a et b sont les paramètres de cette fonction. L'équation y = a . (1 - exp( -b . x)) en est l'équation générale. En remplaçant les lettres a et b (les paramètres) par des valeurs, selon ces valeurs, on obtient différentes courbes (= équations particulières).
- a est la valeur vers laquelle tend y lorsque x tend vers l'infini (asymptote horizontale).
- a . b est la pente de la tangente à la courbe en x = 0. Cette droite coupe l'asymptote horizontale en x = 1/b.
Pour un même a, b indique donc la rapidité de la décroissance de la fonction.
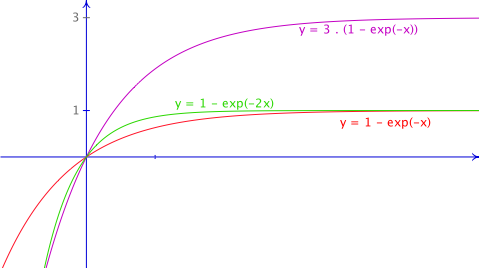
On peut trouver la valeur de 1/b en traçant la tangente à l'origine. Celle-ci coupe l'asymptote horizontale à x = 1/b.
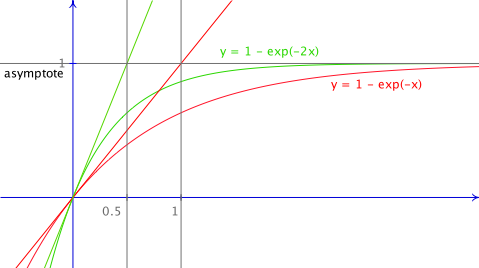
La valeur de 1/b est la valeur de x pour laquelle la grandeur y vaut 0,63 fois sa valeur maximum.
Quand x est le temps, alors 1/b est la constante de temps; c'est le temps au bout duquel la grandeur y vaut 0,63 fois sa valeur maximum.






