Variations des fonctions

• prérequis
• accroissement \( \class{formule}{ Δy }\)
• dérivées \( \class{formule}{ \dfrac{dy}{dx} }\)
• différentielles \( \class{formule}{ dy }\)
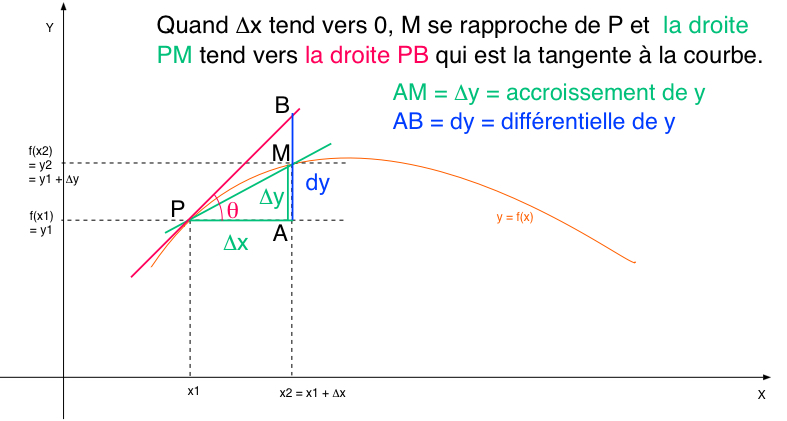
• schéma accroissement, dérivée et différentielle
• fonctions de plusieurs variables (dérivée partielle \( \class{formule}{ \dfrac{∂f}{∂x_1} }\), différentielle partielle \( \class{formule}{ (∂y)_{x_1} }\), différentielle totale \( \class{formule}{ dy }\) )

Prérequis

• les fonctions

Accroissement

Soit une fonction y = f(x).
Lorsque la variable x varie d'une quantité Δx (c.à.d passe de x₁ à x₂ = x₁ + Δx), y = f(x) varie aussi, d'une quantité Δy.
Δx = x₂ - x₁ est appelé l'accroissement de x, Δy = y₂ - y₁ l'accroissement de y.

Dérivée

A part la fonction constante, les fonctions varient d'un point à l'autre, c.à.d que la valeur de y varie d'une valeur de x à l'autre.
Cela peut augmenter plus ou moins vite ou diminuer plus ou moins vite.
Pour décrire mathématiquement comment la fonction varie, il y a ce qu'on appelle la dérivée.

La dérivée d'une fonction en un point donne la variation de cette fonction à cet endroit, ou plus précisément la pente de la droite tangente à la fonction en ce point.

Comme cette pente peut être différente en chaque point, la dérivée de la fonction y(x) est aussi une fonction de x.

De façon plus précise, la dérivée de f par rapport à x, notée f '(x), indique comment se comporte le rapport entre l'accroissement de y (Δy) et celui de x (Δx) lorsque ce dernier devient très petit :
\( \class{formule}{ f '(x) = lim_{Δx→0} \dfrac{Δy}{Δx} }\)

Autre notation pour f '(x) : \( \class{symbol}{ \dfrac{df}{dx}} \)

La dérivée seconde f ''(x) s'obtient en dérivant f '(x) : \( \class{formule}{ f ''(x) = \dfrac{df '}{dx} }\) et se note aussi \( \class{symbol}{\dfrac{d^2f}{dx^2} }\)
Elle indique la concavité de la fonction.

Pour le calcul des dérivées, voir la section des formules.

Utilisation de la dérivée

y' > 0 ⇔ y croissante
y' < 0 ⇔ y décroissante
y' = 0 ⇔ la tangente en ce point est horizontale. Si y' reste nul sur un intervalle ⇒ y cste sur cet intervalle.

y'' > 0 ⇔ concavité tournée vers les y positifs, courbe au-dessus la tangente
y'' < 0 ⇔ concavité tournée vers les y négatifs, courbe sous la tangente
y'' = 0 ⇔ changement de concavité = point d'inflexion

y' = 0 et y'' > 0 ⇔ minimum
y' = 0 et y'' < 0 ⇔ maximum
y' = 0 et y'' = 0 ⇔ point d'inflexion à tangente horizontale

Différentielle

Soit une fonction y = y(x).
Si x varie d'une quantité Δx (c.à.d passe de x₁ à x₂ = x₁ + Δx), de quelle quantité Δy varie y ?
On peut le calculer de façon exacte : on calcule y₁ = y(x₁), puis y₂ = y(x₂), et Δy = y₂ - y₁.
Mais il existe une méthode approchée, plus rapide, et qui donne une très bonne approximation pour des petites variations de x (dx).

On peut montrer que l'accroissement de y ( Δy) peut être calculé comme une somme de 2 termes, en utilisant la dérivée de y par rapport à x :
Δy = y '(x) . Δx + f(Δx)
Le second terme est fonction de Δx et devient négligeable pour de très petits Δx.

Le premier terme est appelé la différentielle de y (noté dy). C'est la valeur vers laquelle tend l'accroissement de y lorsque l'accroissement de x est petit :
dy = lim_Δx→0Δy = y '(x) . Δx
(Pour x, dx = Δx.)

La différentielle permet de calculer simplement une valeur approchée de l'accroissement, approximation d'autant meilleure que Δx est petit.

Fonctions de plusieurs variables

Soit une fonction y de 2 variables : y = f(x₁,x₂).
Si x₁ varie, f variera. Si x₂ varie, f variera aussi.
Lorsqu'on calcule une dérivée ou une différentielle, il faut indiquer pour une variation de quelle variable. Les autres variables sont maintenues constantes.

dérivée partielle : \( \class{symbol}{\dfrac{∂f}{∂x_1}} \class{formule}{= lim_{Δx_1→0} \dfrac{Δy}{Δx_1} }\) avec x₂ cste

différentielle partielle : \( \class{symbol}{ ∂y{_{x_1}}} \class{formule}{ = \dfrac{∂y}{∂x_1} . dx_1 }\), qui est une approximation de l'accroissement partiel de y lors d'un accroissement de x₁mais avec x₂ cste.

On peut aussi avoir toutes les variables qui varient en même temps. La différentielle totale est une approximation de l'accroissement de y lorsque x₁ et x₂ varient simultanément.
différentielle totale : \( \class{symbol}{dy} \class{formule}{= \dfrac{∂y}{∂x_1} . dx_1 + \dfrac{∂y}{∂x_2} . dx_2 }\)