Magnétisme

• prérequis
• définition et unités
• production
• théorème d'Ampère
• effets
• mouvement d'une particule chargée dans un champ magnétique
• dipôle magnétique
• distinction production/effet

Prérequis

• vecteurs (dont l'addition, le produit scalaire et le produit vectoriel),
• intégrales,
• dynamique du point,
• dynamique du solide,
• courant continu.

Définition et unités

Pour la définition du champ magnétique, consultez le lexique.

Unité :

(SI) : le tesla (T)
(CGS): le gauss (G), 1 G = 10^-4 T.

Production de £B

(Pour tous les schémas de cette section, cliquez sur l'icône pour l'agrandir)

Deux grandes causes :

1. orientation des moments magnétiques (orbitaux et de spins) des électrons dans la matière ( aimant permanent )
   
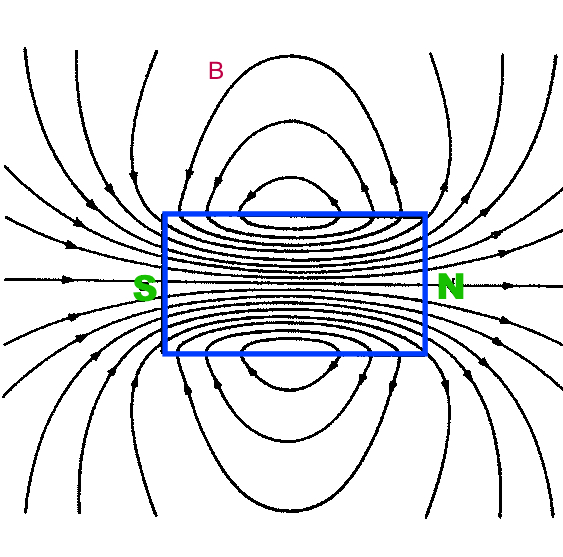2. déplacement de charges électriques (libres ou dans un conducteur)
   

Pour calculer le champ magnétique produit par un déplacement de charges, 2 méthodes possibles :

1. 1. Pour une particule chargée, de charge q et se déplaçant à une vitesse v : \( \class{formule}{ \vec{B} = \dfrac{μ}{4π} . \dfrac{q . \vec{v} Λ \vec{u}_r}{r^2} }\)
      où u_r est un vecteur de longueur 1 orienté selon le vecteur r allant de l'endroit où se trouve la particule au point où on veut calculer £B.
      μ = perméabilité magnétique. Dans le vide : \( \class{formule}{ μ_0 = 4π . 10^{-7} SI = \dfrac{1}{ε_0 . c^2} }\) où c est la vitesse (célérité) de la lumière
      
      
   2. Pour le courant dans un petit morceau de fil conducteur de longueur dl, on remplacera q.v par I . dl. On intègre ensuite sur toute la longueur du conducteur. Cela donne la loi de Biot-Savart : \( \class{formule}{ \vec{B} = \dfrac{μ}{4π} . ∫ \dfrac{I . d\vec{l} Λ \vec{u}_r}{r_2} }\)
      où u_r est un vecteur de longueur 1 orienté selon le vecteur r allant de l'élément de courant I. dl au point où on veut calculer £B.
      
   
   
   
2. le théorème d'Ampère.

Application à quelques cas particuliers

	où	norme	direction	sens règle du tire-bouchon (vis/robinet/...)	schéma (cliquez sur l'icône pour l'agrandir)
fil rectiligne	à une distance d du fil	\( \class{formule}{ B = \dfrac{μ}{4π} . \dfrac{2 . I}{d} }\)	tangent à un cercle centré sur le fil	sens de rotation d'un tire-bouchon qui avance dans le sens du courant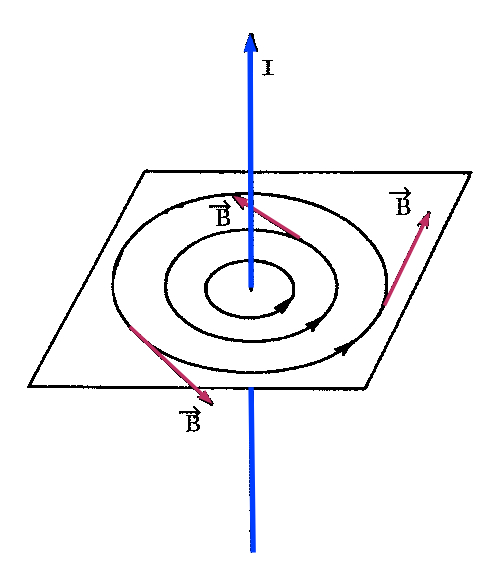
spire (1 boucle)	au centre de la spire de rayon r	\( \class{formule}{ B = \dfrac{μ}{4π} . \dfrac{2 . π . I}{r} }\)	perpendiculaire au plan de la spire	sens de l'avancement d'un tire-bouchon qui tourne dans le sens du courant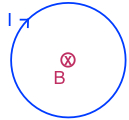
bobine de N spires enroulées sur elles-mêmes	au centre des spires de rayon r	B = N . B(1 sp)	perpendiculaire au plan de la spire	sens de l'avancement d'un tire-bouchon qui tourne dans le sens du courant	idem 1 spire
solénoïde de n spires par unité de longueur	au centre	B = μ . n . I	dans la direction de l'axe	sens de l'avancement d'un tire-bouchon qui tourne dans le sens du courant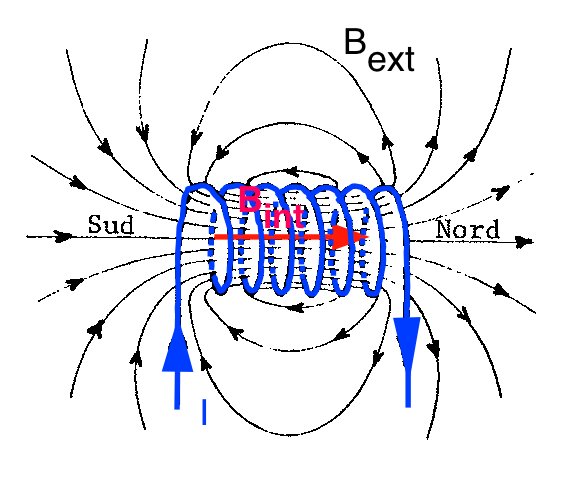

Champ magnétique terrestre

pôle "nord" magnétique (côté pôle nord géographique) = pôle sud magnétique
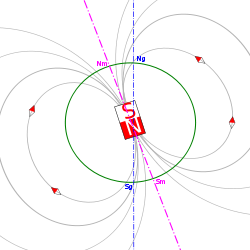
En Belgique, B = 4,8 . 10^-5 T, inclinaison (par rapport à l'horizontale): 66° vers le bas
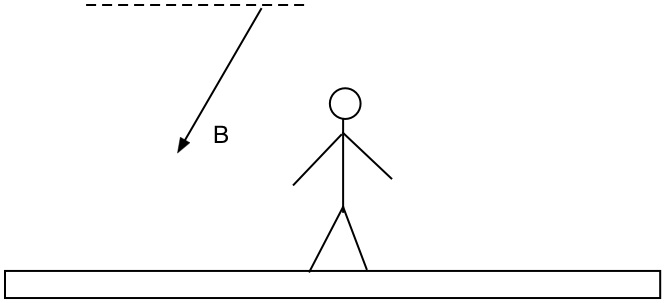
⇒ composante horizontale B_hor = 2 . 10^-5 T

Théorème d'Ampère

La circulation de B sur un contour fermé est égal au produit de la perméabilité magnétique du milieu par le courant total qui passe à l'intérieur de ce contour :

∫ £B • dl = μ . I_int

Pour voir une méthode pour calculer le champ magnétique en utilisant le théorème d'Ampère, cliquez ici.

Effets de B

L'effet n'est que sur les charges en mouvement, et est une force, la force magnétique.

Cette force s'exprime par un produit vectoriel:

• sur des charges libres : £F = q . (v Λ £B)
• sur des charges dans un conducteur rectiligne : £F = I . (l Λ £B) , et si le fil n'est pas rectiligne, £F = ∫ I . (dl Λ £B)

Donc pratiquement :

• sur des charges libres : F = q . v . B . sinθ
• sur des charges dans un conducteur rectiligne : F = B . I . l . sinθ

où θ est l'angle entre v (Il) et £B.

La direction et le sens de F se trouvent par la règle des 3 doigts de la main gauche (ou par votre règle habituelle pour le produit vectoriel).

Mouvement d'une particule chargée dans un champ magnétique

Soit £B uniforme.

Si £B pas uniforme ⇒ le rayon de la trajectoire varie.

Dipôles magnétiques

moment magnétique d'une spire parcourue par un courant : m = I . £S m est parfois aussi noté £μ. Il a le même sens que le £B produit par cette spire. Cette spire = un dipôle magnétique, avec le pôle N du côté vers où pointe m (et £B).

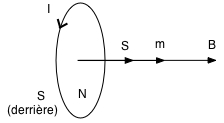moment de force sur un dipôle magnétique dans un champ B externe : £M = m Λ £B_ext

énergie potentielle d'un dipôle magnétique dans un champ B externe : U = - m • £B_ext

flux magnétique à travers une surface : φ = £B_ext • £S
unité: le weber (Wb)

Dans un champ magnétique uniforme, le dipôle tend à s'orienter de façon telle que le flux magnétique soit maximum : son moment magnétique tend à s'aligner avec £B_ext.

Dans un champ magnétique non-uniforme, le dipôle se déplace de façon à maximiser le flux :

• si son moment magnétique est de même sens que £B_ext, le dipôle est attiré par les zones de plus grand £B_ext,
• si son moment magnétique est de sens opposé à £B_ext, le dipôle est attiré par les zones de plus petit £B_ext.

On constate que cela revient à dire que deux pôles de nom contraire s'attirent tandis que deux pôles de même nom se repoussent.

Distinction production/effet

Dans les exercices sur le magnétisme, il faut bien distinguer les deux aspects, production et effet :

1. Qu'est-ce qui produit le champ magnétique ?
   Représenter £B , et si nécessaire, calculer ce que vaut sa norme à l'endroit demandé ou à l'endroit où on cherche son effet (voir plus haut). Pour trouver le sens de £B produit par un courant dans un fil rectiligne ou des spires, on utilise la règle du tire-bouchon (voir tableau ci-dessus).

2. Quel effet a ce champ magnétique ?
   Une force / un moment de force (voir plus haut) ? ATTENTION : c'est uniquement pour trouver le sens de la force qu'on utilise la règle des 3 doigts de la main gauche (voir ci-dessus).