Comme nous l'avons annoncé à la fin de la leçon précédente, nous nous pencherons, dans les 4 leçons suivantes, sur l'écoulement uniforme. Cette leçon-ci est en particulier consacrée à la démonstration de l'équation de base de l'écoulement uniforme (équation de Chézy) et à l'introduction de différentes formules de rugosité qui permettront de modéliser le frottement sur les parois.
ThéorieRappelons tout d'abord les hypothèses de l'écoulement uniforme.
Dans un canal de pente constante et de section transversale invariable (canal cylindrique ou prismatique), l'écoulement est uniforme si :
L'hypothèse de la constance des vitesses concerne bien l'égalité des vitesses moyennes d'une section à l'autre, mais dans une section la vitesse n'est pas obligatoirement constante d'un point à un autre. Souvent, on suppose que la distribution des vitesses est la même d'une section à l'autre, ou alors on néglige les effets de cette distribution.
L'écoulement uniforme peut être laminaire ou turbulent : seul ce dernier cas est d'utilisation courante pour l'ingénieur.
L'écoulement uniforme au sens strict est très rare, mais certains écoulements dans des canaux artificiels peuvent être considérés comme tels. Par exemple, dans un canal artificiel de section et de pente constantes et à condition de se placer suffisamment loin de toute singularité, l'écoulement qui se présente est "à peu près uniforme". C'est souvent le cas dans les canaux d'irrigation (photo ci-contre).
Même dans le cas de rivières naturelles (non strictement prismatiques), on peut utiliser de manière approximative certains résultats du mouvement uniforme, quand la ligne d'eau est sensiblement parallèle au fond.
Enfin, comme nous le verrons, l'écoulement uniforme constitue toujours le régime de référence, même pour les autres types d'écoulement.
Plusieurs auteurs ont décrit l'écoulement uniforme et cela, de différentes façons. Nous verrons essentiellement dans ce cours, les trois formules les plus utilisées : celle de Chézy, de Bazin et de Manning.
La formule de Chézy est la formule "historique" à laquelle la plupart des auteurs font référence, mais à laquelle les praticiens préfèrent des variantes plus précises ou mieux documentées.
Le principe de base de la formule repose sur un équilibre des forces en présence. Supposons un bief élémentaire de longueur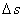 
dans lequel l'écoulement est uniforme.
Remarquons tout d'abord que le canal ou la rivière doivent être prismatique.
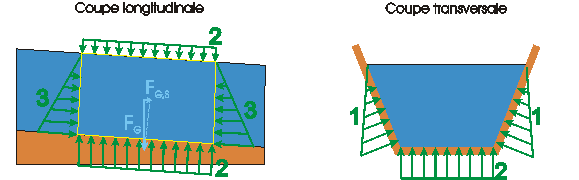
Passons en revue les forces pouvant s'exercer sur l'eau du volume de contrôle de longueur 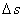ci-dessous et sélectionnons celles qui doivent être prises en compte...
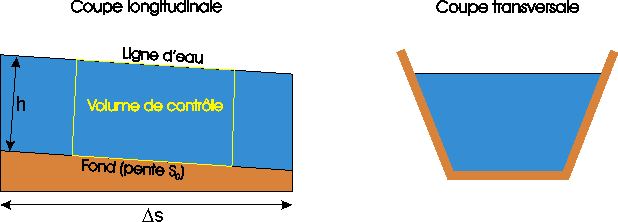
Les forces de gravité (poids propre de l'eau) doivent-elles être prises en compte ?
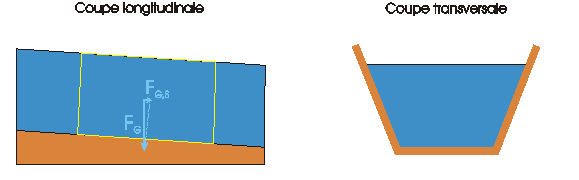
Les forces de pression sur les faces du volume de contrôle sont les suivantes :
L'écoulement rencontre une certaine résistance.
Le frottement contre les parois s'exerce aussi bien sur le fond (ou le lit de la rivière) que sur les berges.
On conclut que les forces à prendre en considération sont :
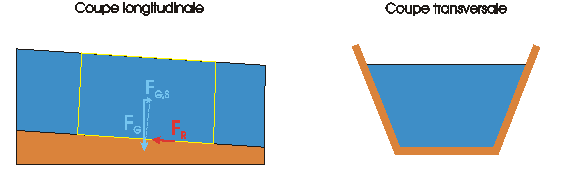
Le théorème de Newton nous apprend que la résultante des forces conduit à une accélération de la masse d'eau :
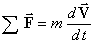
Dans le cas de l'écoulement uniforme, le liquide ne subit aucune accélération, ce qui suppose que les forces sont en équilibre.
Etablissons les résultantes des deux forces à équilibrer.
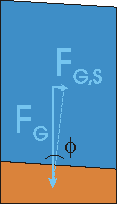
Le poids de l'eau du volume de contrôle vaut :
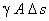
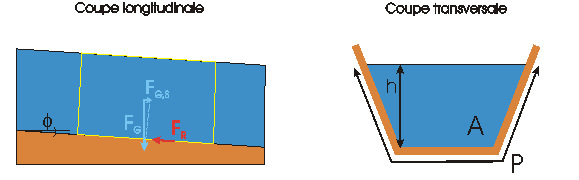
où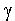 
est le poids volumique. Seule la composante longitudinale doit être prise en compte. On a défini la pente de fond
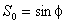
ce qui permet d'écrire la composante longitudinale sous la forme :
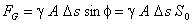
Quant à la force de frottement, opposée à l'écoulement, elle s'exerce sur toute la longueur du périmètre mouillé
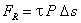
où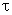 
est la contrainte de frottement par unité de surface.
Comme le régime est turbulent, cette contrainte est proportionnelle au carré de la vitesse moyenne de l'écoulement :
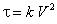
si bien que la force de frottement s'écrit :
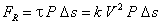
L'équilibre entre la force de gravité, dans le sens de l'écoulement, et la force de frottement, opposée à l'écoulement, s'écrit :
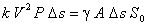
Le rayon hydraulique étant défini, comme nous l'avons vu dans la leçon précédente, par le rapport de l'aire mouillée au périmètre mouillé :
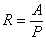
on peut donc déduire la formule de Chézy :
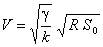
qui s'écrit plus simplement :
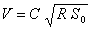
où
La formule de Chézy est souvent prise comme référence dans les traités d'hydraulique, mais elle n'est pas utilisée par les praticiens, et cela pour deux raisons :
Les ingénieurs se sont attachés à trouver un expression de
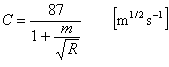
Dans cette formule,
| Nature des parois | |
|---|---|
| Parois très unies (ciment, bois raboté...) | 0,06 |
| Parois unies (planches, briques, pierres de taille...) | 0,16 |
| Parois en maçonnerie de moellons | 0,46 |
| Parois de nature mixte (section en terre, très irrégulières) | 0,85 |
| Canaux en terre dans les conditions ordinaires | 1,30 |
| Canaux en terre, avec fond de galets, parois herbées | 1,75 |
La formule de Chézy, avec le coefficient de Chézy calculé à partir de la formule de Bazin, est utilisée essentiellement dans les pays latins et en France en particulier. Cependant, pour les calculs pratiques, les formules qui suivent sont plus répandues et souvent d'un usage plus simple.
Manning, propose quant à lui une autre formule pour lier le coefficient de rugosité
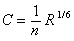
Dans cette formule, la valeur de
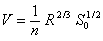
ce qui rend la formule de Manning souvent plus facile à utiliser dans les calculs.
De plus, les tableaux des valeurs de
Nous trouverons, en suivant ce lien un tableau reprenant les valeurs de
La leçon suivante vous permettra de voir comment, pratiquement, utiliser ces formules pour calculer un débit ou une hauteur d'eau. Mais, tout d'abord, quelques exercices du type questions à choix multiples et d'autres de classement vont vous permettre de fixer ces notions importantes.
Langue 
English