Cette dernière leçon traite de trois applications particulières d'écoulement en canaux rectilignes. Vous verrez que ces problèmes ne sont pas sensiblement différents de ceux rencontrés jusqu'ici et que le recourt aux diagrammes de l'énergie spécifique s'avère à nouveau souvent nécessaire.
Résumé théoriquePour mesurer le débit d'un petit canal, on peut le rétrécir localement: la mesure de la hauteur de l'eau avant et dans le rétrécissement (cas du Venturi noyé) ou uniquement avant le rétrécissement (cas du Venturi dénoyé) permet de calculer le débit.
Dans le canal Venturi, la pente de fond est toujours faible ou nulle et les transitions sont conçues pour diminuer les pertes de charge.
Ce cas est similaire à celui de l'écoulement entre piles de pont en faible pente (Leçon V.4) .
On suppose le régime uniforme aux limites.
A l'aval, l'axe
L'évolution dans le rétrécissement est commandée par la variation de la charge spécifique.
A l'amont se produit un axe
L'écoulement est toujours au dessus de la hauteur critique : écoulement noyé. Si on connaît les hauteurs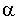 
et
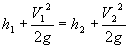
Si 
devant 
et donc le débit s'exprime en fonction de
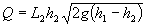
Ce cas est similaire à celui de l'écoulement entre piles de pont en faible pente (Leçon V.4) .
Le passage au droit du rétrécissement nécéssite une accumulation d'énergie spécifique par un axe
Si on néglige la perte de charge et qu'on suppose que le fond est horizontal, alors
Or,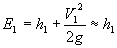 
et, pour un canal rectangulaire, 
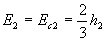d'où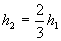 
. En remplaçant dans la formule du débit vue ci-dessus, on peut exprimer le débit à partir de la mesure de
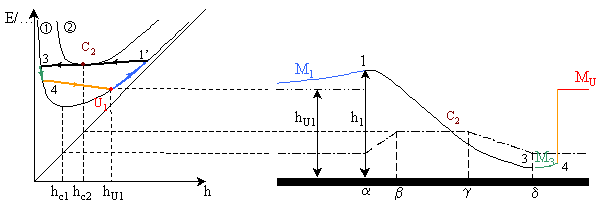
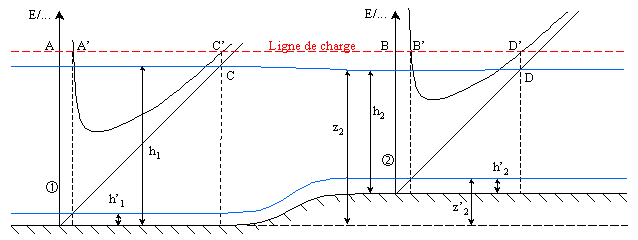
Supposons un canal à fond horizontal avec un relèvement local du fond progressif pour ne pas introduire de pertes de charge : la ligne de charge est donc horizontale.
On dessine les courbes d'énergie spécifiques de part et d'autre du seuil. Faisant coïncider l'origine avec le fond, la courbe représente la charge absolue.
Si le canal est rectangulaire, les courbes seront identiques, la seconde étant translatée de la hauteur du seuil.
Si A' et C' (B' et D') sont les intersections de la courbe 1 (2) et de la ligne de charge, on déduit que AA' < BB' et CC' < DD'.
De AA' < BB', on conclut que
donc, en cas d'écoulement supercritique, le niveau d'eau remonte dans l'absolu sur un seuil (
De CC' < DD', On déduit qu'en cas d'écoulement subcritique, le niveau
Un seuil de fond accélère un écoulement subcritique, au point que son niveau baisse dans l'absolu, et décélère un écoulement supercritique.
Pour éviter le ressaut, la hauteur de seuil ne doit pas être telle que la hauteur de charge disponible soit inférieure à l'énergie spécifique minimum dans la section 2.
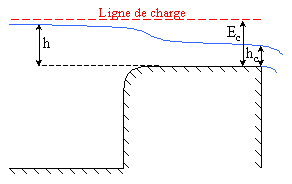
Si l'écoulement est dénoyé (c'est-à-dire si le niveau à l'aval est nettement inférieur au seuil du déversoir), la hauteur critique se produit au voisinage de l'arête aval du déversoir (énergie spécifique minimum pour le débit du déversoir).
Or, dans un canal rectangulaire en régime critique,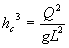 
et 
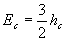d'où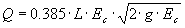 
Sur le seuil, on constate un abaissement de l'axe (comme pour un écoulement subcritique avec seuil de fond), tandis qu'à l'amont, l'axe tend vers hu ou le niveau du réservoir (si i=0). On remarque que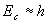 
de sorte que :
Langue 
English