Hypothèses de base

On suppose que l'écoulement est :

• Permanent : Un cliché photographique des hauteurs d'eau, des vitesses, des débits, serait le même, quel que soit le moment de la prise de vue. On en déduit que les dérivées partielles de toutes les grandeurs physiques par rapport au temps sont nulles, et que les trajectoires ne se distinguent pas des lignes de courant. Si, en un point donné, les hauteurs d'eau ne varient pas avec le temps, elles peuvent, par contre, être différentes d'un point à un autre.


• Continu : Le débit est le même dans toute section de la rivière ou du canal.
  Cette hypothèse permet-elle de prendre en compte un affluent ?
  
  Oui

  Faux ! Cette hypothèse ne permet pas de prendre en compte un affluent, puisque le débit est considéré comme constant sur toute la longueur du canal.

  Non

  Correct ! Cette hypothèse ne permet pas de prendre en compte un affluent, puisque le débit est considéré comme constant sur toute la longueur du canal.
  
  Cette hypothèse permet-elle de prendre en compte le ruissellement venant des flancs de la vallée ?
  
  Oui

  Faux ! Cette hypothèse ne permet pas de prendre en compte le ruissellement venant des rives, car ce ruissellement peut être considéré comme un débit alimentant le cours d'eau, or on a fait l'hypothèse d'un débit constant.

  Non

  Correct ! Cette hypothèse ne permet pas de prendre en compte le ruissellement venant des rives, car ce ruissellement peut être considéré comme un débit alimentant le cours d'eau, or on a fait l'hypothèse d'un débit constant.

• Bidimensionnel : Cette troisième hypothèse, valable pour la plus grande partie de ce cours, suppose que l'écoulement est plan. Même s'il est tenu compte de la largeur du cours d'eau et de la forme de son profil en travers pour le calcul de l'écoulement, on considérera que le niveau d'eau ne varie pas transversalement. Chaque section est donc représentée par un seul niveau d'eau, ce qui permet de dessiner la ligne d'eau (ou axe hydraulique) dans une coupe longitudinale de la rivière.

Au vu de cette dernière hypothèse, qui nous permet de dessiner une coupe longitudinale de l'écoulement, se pose un problème de représentation. Il va nous falloir choisir un système d'axes de référence adéquat et pratique. C'est ce que nous allons voir dans les pages suivantes.

Systèmes d'axe de référence

Nous venons de le voir, nous pouvons travailler sur une coupe longitudinale... Un problème va néanmoins apparaître. En effet, regardons la figure ci-dessous, c'est une représentation, à l'échelle, d'un bief de 3 km de long, bief dans lequel la profondeur d'eau est d'environ 4 m.

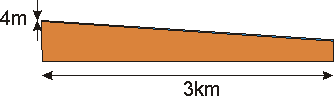
La conclusion est évidente : il nous faut utiliser une échelle distordue, c'est-à-dire différente pour les longueurs et les profondeurs, pour "voir" quelque chose... Nous obtenons ainsi une représentation beaucoup plus claire :

Néanmoins, travailler avec une échelle distordue ne va pas sans poser de problème. En effet, si l'on veut être rigoureux :

• La hauteur d'eau ne doit pas être représentée perpendiculairement au fond;
  
  Pourquoi

  Parce que, dans un graphe distordu, les angles ne sont pas conservés.


• Ni verticalement;
  
  Pourquoi

  Parce que, si le canal a une pente de fond, la perpendiculaire au fond n'est pas verticale. Or seules les verticales sont vues comme verticales dans un graphe distordu.


• Mais par une oblique qui n'est ni perpendiculaire au fond, ni verticale.
  
  Comment

  Par exemple, en traçant sur le graphe la représentation de deux points de la normale au fond.

Dans la pratique, toutefois, cette direction légèrement oblique sera souvent dessinée comme perpendiculaire au fond : la représentation n'est pas rigoureuse mais elle permet de mettre en évidence que la profondeur d'eau n'est pas comptée verticalement. Deux représentations sont donc possibles :

Système classique Oxyz	Système associé au fond de la rivière Osyh
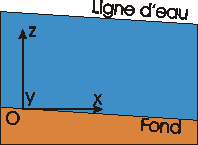Ox est une horizontale longitudinale, Oy est une horizontale transversale et Oz est une verticale. Cette dernière direction est donc représentée par une verticale. Ce premier système est plus proche de la réalité, mais n'est pas vraiment pratique à utiliser (nous le verrons lors de l'établissement des équations de base de l'écoulement)...	La coordonnée 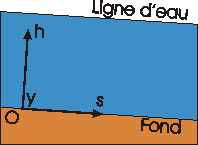s est l'abscisse courante de la rivière et h la distance au fond comptée perpendiculairement à celui-ci. (dans une rivière sinueuse, s suit le thalweg). Ce deuxième système est beaucoup plus facile à utiliser, mais il n'est pas exact. Néanmoins, il insiste sur le fait que h n'est pas verticale !

Ces deux systèmes d'axes de références sont-ils forts différents ? Non, si nous faisons l'hypothèse d'une pente de fond faible. Nous utiliserons donc le système associé au fond de la rivière Osyh, tout en sachant que c'est une représentation fausse, mais plus pratique !

Régimes d'écoulement à surface libre

Cote piézométrique, charge, nombre de Reynolds

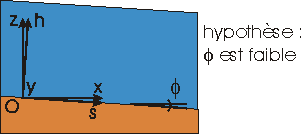
Pour décrire l'écoulement, nous devons introduire un certain nombre de paramètres. Le plus simple est de définir ceux-ci par référence à leur équivalent en hydraulique des conduites (écoulement en charge).

Pour rappel, dans un écoulement en conduite, si on admet l'hypothèse d'un écoulement parallèle, on peut dire que la cote piézométrique H :

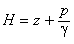
est constante dans une section donnée. Dans le cas d'une conduite la cote piézométrique est donc le niveau atteint dans un tube piézométrique.

Quant à la charge :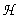

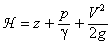
elle représente le niveau énergétique de la section considérée.

La perte de charge :

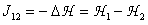
ne peut qu'être positive, si l'écoulement va de la section 1 vers la section 2.

Les mêmes grandeurs sont choisies pour représenter un écoulement à surface libre (attention : la figure est distordue, on suppose que la pente de fond est assez faible pour envisager la profondeur h comme verticale...). L'écoulement est supposé parallèle également, si bien que le niveau piézométrique est le même en tout point d'une section transversale et donc égal à la cote de la surface libre, où règne la pression atmosphérique. En utilisant le coefficient de distribution de vitesse (coefficient de Coriolis), on peut utiliser la vitesse moyenne V pour représenter l'énergie cinétique moyenne.

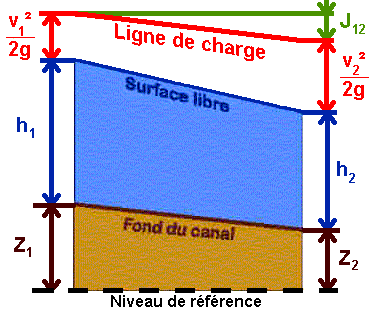
Comme la cote piézométrique est unique pour tous les points d'une section et que l'énergie cinétique est moyennée sur la verticale, on peut considérer qu'en une section, la charge est définie de manière univoque. Comme dans les conduites, l'écoulement peut être laminaire, turbulent ou de transition et dépend de la viscosité représentée par le nombre de Reynolds :

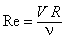
où 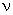V est la vitesse moyenne du fluide, R le rayon hydraulique (au lieu du diamètre de la conduite) et la viscosité cinématique (pour l'eau : environ 10^-6 m²/s).

Nous le remarquons : le nombre de Reynolds dépend du rayon hydraulique. Que recouvre exactement cette notion ? En conduite, la longueur significative est le diamètre; en écoulement à surface libre, c'est le rayon hydraulique qui joue ce rôle.

Le rayon hydraulique est défini comme le rapport de l'aire mouillée au périmètre mouillé :

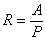
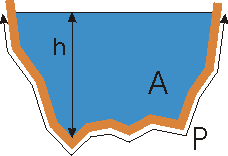
où l'aire mouillée A représente la surface offerte à l'écoulement, tandis que le périmètre mouillé P est une mesure de la résistance à l'écoulement par frottement. A une surface régulière (P petit), correspondra un rayon hydraulique R plus grand; à une surface irrégulière (P grand), correspondra un rayon hydraulique R plus petit. Nous verrons que cette différence joue un rôle dans la relation débit - profondeur d'eau.

La notion de profondeur, dans un cadre unidimensionnel, mérite d'être précisée, surtout dans le cas d'une rivière naturelle, où le lit est loin d'être régulier. On choisit de définir la profondeur h là où le niveau du lit est le plus bas dans la section (figure ci-dessus), c'est-à-dire au droit du thalweg, ce dernier étant défini comme le lieu des points bas de la rivière.

Régimes hydrauliques

Nous pouvons distinguer trois types d'écoulement en fonction de l'évolution de la profondeur h dans le canal ou la rivière et de la variation correspondante des vitesses moyennes ;

• Si la profondeur ne varie pas le long du canal (la pente de la ligne d'eau est donc égale à la pente de fond), on dira que l'écoulement est UNIFORME. Les vitesses moyennes sont constantes d'une section à l'autre. Au sein d'une section elles sont parallèles, mais peuvent varier d'un point à un autre. On retrouve le même champ de vitesses d'une section à l'autre.


• Si la profondeur et, avec elle, les vitesses moyennes, varient d'une section à l'autre, mais de manière progressive, on parlera d'écoulement ou de régime GRADUELLEMENT VARIE.


• Si le changement est important ou localisé, on parlera d'écoulement ou de régime BRUSQUEMENT VARIE.

Cette distinction ne dépend absolument pas des variations de forme du canal. Un écoulement brusquement varié peut se produire en un point du canal présentant également une variation brutale de section ou de pente mais aussi dans un canal prismatique, loin de telles modifications de section.

Par contre, un écoulement uniforme n'est pas possible dans un canal non prismatique.

Nous étudierons ces trois régimes successivement, les leçons du chapitre II traitant de l'écoulement uniforme, les leçons du chapitre III du régime graduellement varié, et les leçons suivantes de l'écoulement brusquement varié. Des applications seront proposées pour ces différents cas et permettront d'y voir progressivement plus clair.

Auparavant, quelques exercices du type QCM (questions à choix multiples) vont vous permettre de tester vos connaissances à l'issue de cette première leçon. Vous y accéderez en cliquant sur l'icône "questions théoriques" du menu à gauche de la leçon...