Dynamique - résolution de problèmes de calcul de pressions en hydrostatique

Voici une aide pour résoudre les problèmes de calcul de pressions en hydrostatique. Libre à vous de suivre ces indications, de les adapter, de les simplifier (avec un peu d'habitude, vous ferez plusieurs de ces étapes mentalement).

Dans un problème où l'on doit calculer la pression hydrostatique à un endroit donné ou la hauteur d'un liquide (du type tube en U par exemple), on attribue un chiffre ou une lettre aux différents endroits clés du problème : par exemple,

• au-dessus de la surface du liquide,
• de part et d'autre d'une surface de séparation (soit entre 2 liquides différents ou entre un liquide et un gaz),
• à la même hauteur qu'à un autre endroit dans le même liquide...
• à une autre profondeur dans le même liquide.

On calcule ensuite les pressions hydrostatiques p_i à ces différents endroits, en partant d'un point de pression connue, puis les uns par rapport aux autres, en appliquant le théorème de Bernoulli ou une de ses conséquences, ou la théorie sur les capillaires (surface concave, convexe ou plane).

Exemple

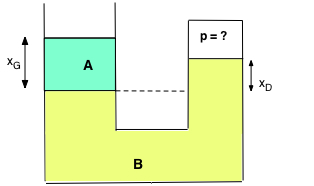On connait les hauteurs xG et xD et les masses volumiques des liquides A et B. Que vaut la pression de l'air à droite dans l'espace au-dessus du liquide B ?

Résolution

On attribue des chiffres à différents endroits clés du problème :

On calcule les pressions en ces différents points, en commençant par p1 qui est connue :

p1 = patm (point au-dessus de la surface, tube ouvert)
p2 = p1 car tube large ⇒ surface plane
p3 = p2 + ρ_A . g . x_G (conséquence du théorème de Bernoulli, et x_G est l'augmentation de profondeur entre 2 et 3 - voir dessin)
p4 = p3 car tube large ⇒ surface plane
p5 = p4 (conséquence du théorème de Bernoulli : points à la même hauteur H dans le même liquide)
p5 = p6 + ρ_B . g . x_D (conséquence du théorème de Bernoulli, et x_D est l'augmentation de profondeur entre 6 et 5 - voir dessin)
p7 = p6 car tube large ⇒ surface plane