Comment calculer la norme d'un produit vectoriel

Soit le produit vectoriel c = a Λ b .

Voici quatre façons de calculer la norme de ce produit, c :

1. c = a . b . sinθ	où θ est l'angle entre les vecteurs a et b
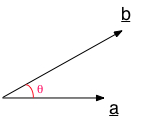2. c = aperp . b	où aperp est la composante de a perpendiculaire à b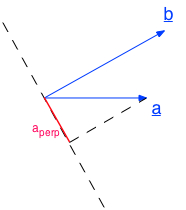
3. c = a . bperp	où bperp est la composante de b perpendiculaire à a
4. c = | ax . by - ay . bx |	pour les composantes de ces vecteurs selon 2 axes orthogonaux X et Y.

Le choix de la méthode se fera, comme d'habitude, de manière à avoir des calculs simples et courts, et dépend donc de ce qu'on connait.

Orientation du vecteur c :

• direction perpendiculaire à a et à b (donc au plan défini par ces 2 vecteurs)
• sens : règle du tire-bouchon (robinet, vis...); lorsque les vecteurs ont même origine, on fait tourner le premier vecteur vers le second par le côté où c'est le plus court, et le sens de c est le sens dans lequel le tire-bouchon se déplace.