Thermodynamique

• prérequis
• 1er principe de thermodynamique
• quelques transformations particulières
• aide à la résolution de problèmes
• cycle de Carnot
• rendement
• entropie
• enthalpie, enthalpie libre

Prérequis

• hyperbole,
• intégrales,
• énergie,
• théorie cinétique des gaz,
• calorimétrie

1ier principe de la thermodynamique

Soit un système fermé.

W = travail fournit (reçu) par le système = ∫ P . dV

Q = quantité de chaleur donnée (reçue) par le système

Il y 2 cas pour lesquels on dispose d'une formule :

• transformations isochores : C_V . n . Δt
• transformations isobares : C_P . n . Δt

U = énergie interne = fonction d'état

ΔU = variation de l'énergie interne = C_V . n . Δt

Quelques transformations particulières

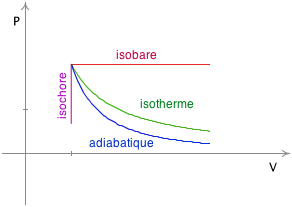
isotherme : T = cste et on a P . V = cste isochore : V = cste isobare : P = cste adiabatique : Q = 0 et on a P . Vγ = cste où \( \class{formule}{ γ = \dfrac{C_P}{C_V} }\) cycle : l'état final est le même que l'état initial (même P, V, T, n)

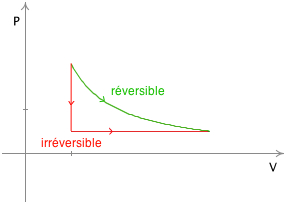
transformation réversible : transformation où tous les états intermédiaires sont des états d'équilibre. Ils obéissent tous à la loi des gaz parfaits. ⇒ isotherme : branche d'une hyperbole   transformation isotherme irréversible : Ti = Tf mais elle ne reste pas cste entre i et f. La transformation peut se réaliser, par exemple, par une isochore suivie d'une isobare.

Cycles

• cycle isotherme réversible : W_tot = 0, Q_tot = 0
• cycle isotherme irréversible : W_tot < 0, Q_tot < 0

Vous pouvez vous inspirer de cette aide à la résolution de problèmes.

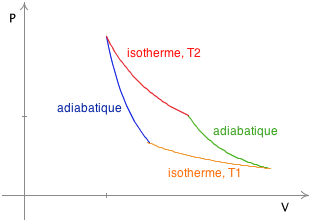
Cycle de Carnot : détente isotherme réversible à T2, Q2 fourni par l'extérieur, détente adiabatique réversible de T2 à T1 < T2, compression isotherme réversible à T1, Q1 rejeté vers l'extérieur, compression adiabatique réversible de T1 à T2.

Rendement d'un moteur

Le rendement r = énergie produite / énergie fournie \( \class{formule}{ = \dfrac{W_{tot}}{Q_2} = 1 + \dfrac{Q_1}{Q_2} }\)

• pour un cycle réversible \( \class{formule}{ r = 1 - \dfrac{T_1}{T_2} }\)
• pour un cycle irréversible \( \class{formule}{ r' < 1 - \dfrac{T_1}{T_2} }\)

Entropie

Soit un système fermé.

L'entropie S est une fonction d'état.

\( \class{formule}{ ΔS = ∫ \dfrac{dQ_{rév}}{T} }\) ne dépend que des états i et f.

• ΔS = 0 si transformation réversible
• ΔS > 0 si transformation irréversible

Enthalpie - enthalpie libre

On définit aussi une autre fonction d'état, l'enthalpie H = U + P . V

A P cste, ΔH = Q ⇒ surtout utilisée en chimie pour caractériser les réactions chimiques :

ΔH < 0 : réaction exothermique, chaleur dégagée
ΔH > 0: réaction endothermique, chaleur absorbée

H fonction d'état ⇒ loi de Hess : La variation d'énergie des processus chimiques ou physiques est indépendante du chemin suivi ou du nombre d'étapes nécessaires pour compléter le processus tant que les états initial et final de la réaction sont les mêmes.

Pour un système non-isolé, il est plus pratique d'utiliser encore une autre fonction d'état, l'enthalpie libre G.
G = H - T . S

Pour les transformations avec P et T constantes (comme celles se produisant dans l'air): ΔG = 0.
En général : ΔG ≤ 0