Théorie cinétique des gaz

• prérequis
• gaz parfaits
• vitesses des molécules
• pression, volume et énergie cinétique en fonction de la température
• mélange de gaz
• gaz réel: formule de Van der Waals

Prérequis

• énergie,
• collisions,
• hydrostatique

Gaz parfaits

1. taille des molécules telle qu'on peut les considérer comme des points géométriques,
2. molécules indépendantes les unes des autres,
3. chocs entre les molécules parfaitement élastiques

Vitesses des molécules

vitesse la plus probable : vp vitesse moyenne : \( \class{formule}{ \class{symbol}{v_m} = \dfrac{∑ n_i . v_i}{n} }\) vitesse quadratique moyenne : \( \class{formule}{ \class{symbol}{\overline{v}} = \sqrt{\dfrac{∑ n_i . v_i^2}{n}} }\)

distribution selon la loi de Maxwell-Boltzmann ⇒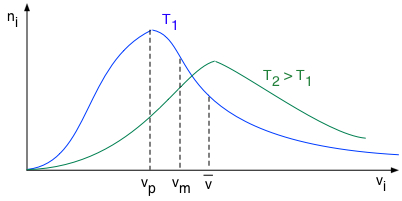

\( \class{formule}{ v_p = \sqrt{ \dfrac{2 . k . T }{m}} }\) \( \class{formule}{ v_m = \sqrt{ \dfrac{8 . k . T }{π . m}} }\) \( \class{formule}{ \overline{v} = \sqrt{\dfrac{3 . k . T}{m}} }\)

énergie cinétique totale : \( \class{formule}{ E_K = \dfrac{M . \overline{v}^2}{2} }\)

pression : \( \class{formule}{ P = \dfrac{1}{3} . ρ . \overline{v}^2 }\)

Pression et volume en fonction de la température :

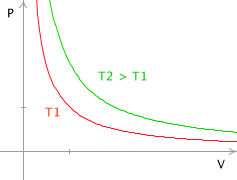
1) A température constante loi de Boyle-Mariotte : P . V = cste

2) Effets de la chaleur sur les gaz

loi des gaz parfaits : P . V = n . R . T

• T₀ = 273 K, P₀ = 1 atm, V₀ = 22,4 l,
• R = cste des gaz parfaits = 0,082 l.atm/mol.K = 8,31 J/mol.K = 1,98 cal/mol.K

Energie cinétique d'une mole : \( \class{formule}{ E_K = \dfrac{3}{2} . R . T }\)

• Energie cinétique d'une molécule : \( \class{formule}{ E_K = \dfrac{3}{2} . k . T }\)
• où k = cste de Boltzmann \( \class{formule}{ = \dfrac{R}{N} }\)
• et N = nbre d'Avogadro = 6 . 10²³

Mélange de gaz

Soit un gaz i d'un mélange, caractérisé par son nombre de moles n_i, son volume partiel V_i, sa pression partielle P_i.
Pour le mélange, n = ∑ n_i

On définit :

Et on montre les relations suivantes :

• P = ∑ P_i ,V = ∑ V_i
• \( \class{formule}{\dfrac{V_i}{V} = \dfrac{n_i }{n} }\)
• \( \class{formule}{ P_i = P . \dfrac{n_i}{n} = P . \dfrac{V_i}{V} }\)

Formule de van der Waals

⇒ la loi des gaz parfaits doit être modifiée :

b est le volume occupé par les autres molécules, appelé covolume.