Dynamique - hydrodynamique

Hydrodynamique : v ≠ 0

• prérequis
• Tout comme en hydrostatique, on distinguera 2 types de problèmes :
  1. on étudie un objet se déplaçant dans un fluide
  2. on étudie l'écoulement du fluide.

Prérequis

• la dynamique du point,
• l'énergie,
• l'hydrostatique.

1. Etude d'un objet se déplaçant dans un fluide

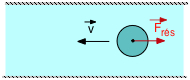
On appliquera toujours la seconde loi de Newton, ∑£F = m . a, avec une nouvelle force supplémentaire :

la force de résistance au cheminement (ou force de frottement visqueuse) : F_rés = C . (1/2) . ρ v² S
= force sur un objet se déplaçant dans un fluide, v = vitesse relative objet-fluide

La valeur de C (coefficient de résistance, nombre pur) dépend de la valeur du nombre de Reynolds \( \class{formule}{ \class{symbol}{R} = \dfrac{ρ . v . d}{η} }\) :

• Si R < 1 ⇒ \( \class{formule}{ C = \dfrac{24}{R} }\) ⇒ F ∝ v : F = f . v où f (aussi noté γ ou β et appelé coefficient d'amortissement dans les problèmes de d'oscillations amorties). Pour une sphère de rayon r, F peut se réécrire F_rés = 6 . π . η . v . r (formule de Stokes)
  
• Si \( \class{formule}{ 500 < R < 200 000 }\) ⇒ F ∝ v², et C= 1,2 (cas du parachutiste)

Conséquence de cette force

Un corps se déplaçant dans un fluide va atteindre, après un certain temps, une vitesse constante ( appelée "vitesse limite").

• Pour \( \class{formule}{ R < 1 }\), c'est la sédimentation. La vitesse limite est appelée vitesse de sédimentation (on peut retrouver facilement la formule en appliquant la 2ième loi de Newton). graphe v(t)
• Pour de grands R, le corps peut aussi atteindre une vitesse limite (exemple : un parachutiste graphe v(y)).
  

2. Etude de l'écoulement d'un fluide

Définition : le débit D = S . v

Pour un fluide parfait,

c.à.d. incompressible et non visqueux (sans frottement), on a :

1. D = cste (équation de continuité)
   
2. conservation de l'énergie ⇒ : \( \class{formule}{ p + ρ . g . h + \dfrac{ρ . v^2}{2} = cste }\) (dans l'espace) C'est le théorème de Bernoulli.
   

Pour a, il suffit d'avoir un fluide incompressible.
Pour b, il faut en plus qu'il soit non visqueux, et que l'écoulement soit laminaire et régulier.

• p est la pression hydrostatique (ou pression) : \( \class{formule}{ p = \dfrac{E_{press}}{V} }\).
• Le terme ρ . g . h , qui est l'énergie potentielle d'une unité de volume, est appelé la pression de pesanteur ou pression de gravitation.
• Le terme \( \class{formule}{ \dfrac{ρ . v^2}{2} }\), qui est l'énergie cinétique d'une unité de volume, est appelé la pression cinétique.
  
• La somme de ces 3 termes, qui est l'énergie totale d'une unité de volume est appelée pression totale.

Pour un fluide réel, écoulement laminaire

• Si fluide pas incompressible, alors le débit n'est plus constant.
• Si le fluide est visqueux, alors on a une nouvelle force : la force de viscosité : \( \class{formule}{ F = η . S . \dfrac{dv}{dx} }\)

C'est une force qui agit sur le liquide en déplacement.
η est appelé le coefficient de viscosité, unité SI : le Poiseuille (Pl)

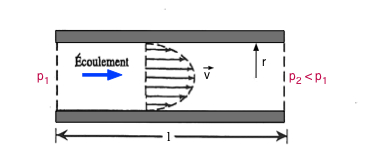
Elle agit comme une force de frottement ⇒ perte d'énergie

⇒ perte de pression Δp = R . D
avec \( \class{formule}{ R = \dfrac{8}{π} . \dfrac{l . η}{r^4} }\) = résistance hydraulique

Pour maintenir l'écoulement, il faut une pompe dont la puissance vaut \( \class{formule}{ P = \dfrac{dW}{dt} = Δp . D }\)

Pour plusieurs canalisations identiques, les résistances hydrauliques se combinent :

• Parallèle : même Δp, \( \class{formule}{ D = ∑D_i }\) , \( \class{formule}{ \dfrac{1}{R} = ∑\dfrac{1}{R_i} }\)
• Série : même débit, \( \class{formule}{ Δp = ∑Δp_i }\) , \( \class{formule}{ R = ∑R_i }\)

On peut faire un parallèle avec le courant électrique qui traverse une résistance (voir ici).

Lignes de charge

On peut représenter les différentes formes d'énergie par unité de volume (donc les différentes formes de pression) divisées par (ρ . g) (= la charge), en fonction de la distance au début de la canalisation.
C'est ce qu'on appelle les lignes de charge.
La charge a les dimensions d'une longueur.
Ce qu'on appelle perte de charge, c'est la perte de pression par frottement visqueux divisée par (ρ . g).
La représentation des lignes de charge montre comment se répartissent les différentes formes d'énergie (les différents termes du théorème de Bernoulli) tout au long de l'écoulement du fluide. Voir l'exemple

Types d'écoulements

Le nombre de Reynolds \( \class{formule}{ R = \dfrac{ρ . \overline{v} . d}{η} }\) sert ici à caractériser le type (ou régime) d'écoulement :

R < 2400 ⇒ écoulement laminaire

R >> 2400 ⇒ écoulement turbulent