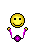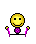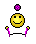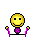Dérivées - fonctions dérivées de fonctions
Prérequis
Présentation
Il y a 2 animations sur cette page.
Première animation
Dans cette vidéo, vous voyez
- une fonction f(x),
- un point A sur la courbe,
- la tangente à la courbe en A,
- la pente de cette droite (qui vaut la dérivée de f en A).
- On regarde l'évolution de cette tangente et de sa pente (donc de la dérivée) en fonction de l'abscisse du point A (en fonction de x).
- On obtient ainsi la fonction dérivée f '(x).
Pour construire vous-même une autre fonction, et sa fonction dérivée, utilisez GeoGebra (application ou version en ligne), en vous inspirant des éléments ci-dessous.
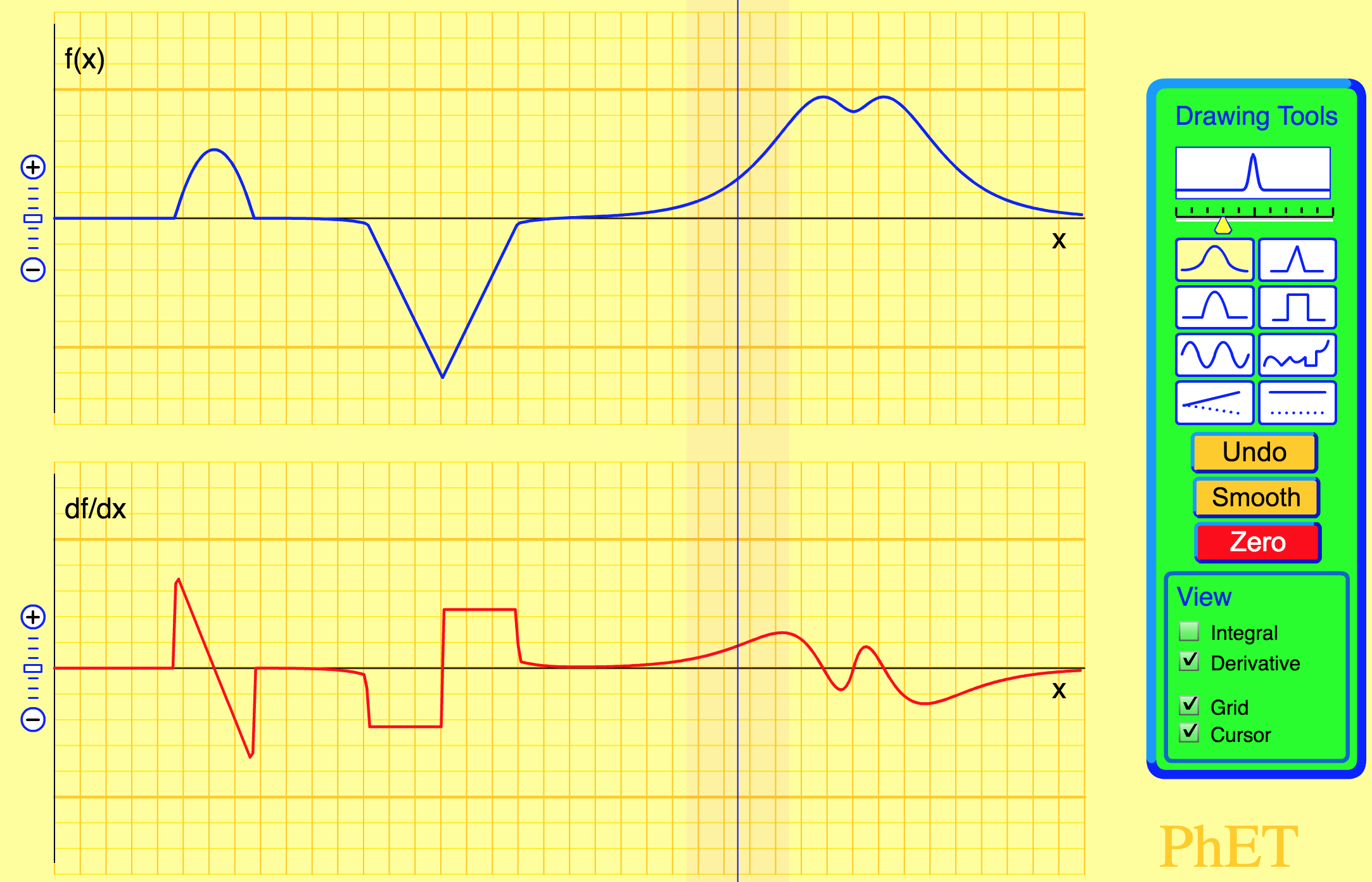
Seconde animation
L'animation ci-dessous vous permet de créer une fonction et d'observer sa dérivée.
Cochez les cases "Grid" et "Cursor" pour une observation plus précise.
Vous pouvez choisir 8 différents types de fonctions.
Pour chaque manipulation proposée ci-dessous, essayez d'abord de prédire quel sera le résultat, et ensuite vérifiez-le à l'aide de l'animation.- Commencez par une droite horizontale (la fonction y = cste). Comment pensez-vous que sera le graphe de sa dérivée ? Vérifiez à l'aide de l'animation.
- Choisissez ensuite une droite non constante, croissante. Comment sera le graphe de sa dérivée ? Augmentez la pente. Comment va changer la dérivée ? Tracez ensuite une droite décroissante.
- Et que va donner la dérivée d'une fonction sinusoïdale ? Utilisez la ligne verticale pour repérer exactement une abscisse donné pour les deux courbes.
- Finalement, vous pouvez essayez les autres formes de courbes, et repérer les zones croissantes, les zones décroissantes, les zones constantes, les changements de pente, ...
auteur : Simulations interactives PhET à l'Université du Colorado Boulder