Fonctions - la droite
Prérequis
y = a . x + b
où
- x est la variable indépendante,
- y est la variable dépendante, et
- a et b sont des constantes (les paramètres de l'équation).
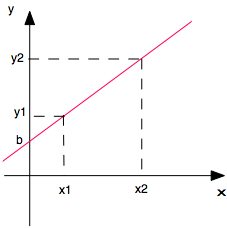
L'équation y = a . x + b est l'équation générale d'une droite.
En remplaçant les lettres a et b (les paramètres) par des valeurs, selon ces valeurs, on a différentes droites (= équations particulières).
b = ordonnée à l'origine (c.à.d. valeur de y à x = 0)
a = pente de la droite = \( \class{formule}{ \dfrac{Δy}{Δx} }\) , c.à.d. \( \class{formule}{ \dfrac{y_2 - y_1}{x_2 - x_1} }\) (encore appelée coefficient angulaire ou coefficient directeur)
a = pente de la droite = \( \class{formule}{ \dfrac{Δy}{Δx} }\) , c.à.d. \( \class{formule}{ \dfrac{y_2 - y_1}{x_2 - x_1} }\) (encore appelée coefficient angulaire ou coefficient directeur)
Si a > 0, la droite est croissante, si a < 0, elle est décroissante.
Elle coupe l'axe des X en 0 ou 1 point, appelé la racine (résoudre y = 0 = a . x + b pour la trouver).
On dit que y est linéairement dépendant de x.
Dans le cas particulier où b = 0, y est proportionnel à x (c.à.d que le rapport y/x est constant, ou encore que si x est multiplié par un facteur n, y sera multiplié par le même facteur).






