Réfraction
Prérequis
- optique : l'onde lumineuse,
- la réflexion
Lois de la réfraction
ou lois de Snell-Descartes pour la réfraction|
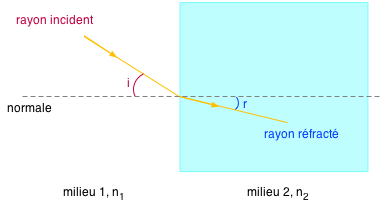
1) rayon incident, normale et rayon réfracté dans un même plan 2) le rayon incident et le rayon réfracté sont situés de part et d'autre de la normale, 3) n1 . sin i = n2 . sin r n = indice de réfraction \( \class{formule}{ = \dfrac{c}{v} }\), dépend de la fréquence de l'onde lumineuse. |
 |
Notes importantes :
- Dans ce cours, les angles sont mesurés par rapport à la normale (voir schéma ci-dessus).
- r désigne tantôt l'angle réfléchi tantôt l'angle réfracté, selon le contexte. Ici, il s'agit bien sûr de l'angle réfracté.
Réflexion totale
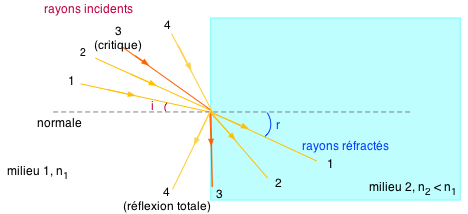
Lorsque n2 < n1, alors r > i (le rayon s'écarte de la normale). Si i augmente, r augmente. On peut arriver à r = 90° ⇒ ne peut être plus grand.
L'angle i correspondant est appelé angle critique.
Si i > i critique ⇒ toute la lumière est réfléchie = réflexion totale.
Prismes
En traversant un prisme, la lumière subit au minimum deux réfractions, parfois une réfraction suivie d'une réflexion totale puis d'une réfraction.
Convention : tous les angles situés à l'extérieur du prisme sont notés i, tous ceux à l'intérieur r.
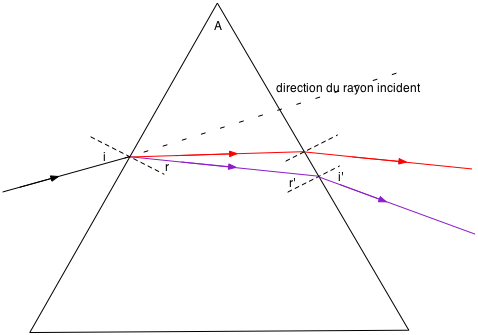
Déviation totale D = angle entre le rayon qui entre dans le prisme et celui qui en sort.
Elle dépend de l'angle d'incidence.
La déviation totale est minimum si i = i' (notée Dm). Elle dépend de l'indice de réfraction n du prisme et de l'angle au sommet A.
Elle permet de calculer n : \( \class{formule}{ n = \dfrac{sin(A + D_m)/2}{sin(A/2)} }\)
Lentilles 
Image d'un objet
Vision directe, image réelle, image virtuelle : voir ici
Construction de l'image d'un objet
i l'objet est sur l'axe optique, cherchez l'image de son autre extrémité. Pour cela, faites la construction géométrique pour deux rayons lumineux particuliers (voir ici).
Là où les rayons réfléchis se croisent se trouve l'image réelle de ce point. Si ces rayons divergent, leurs prolongements se croisent; à cet endroit se trouve l'image virtuelle du point.
Relations utiles
\( \class{formule}{ \dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v} }\) * \( \class{formule}{ G = \dfrac{I}{O} = \dfrac{|v|}{|u|} }\) |
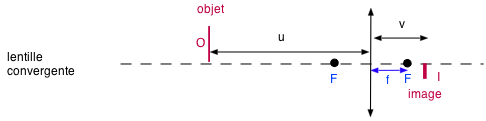 |
\( \class{formule}{ \dfrac{1}{f} = (\dfrac{n_{int}}{n_{ext}} - 1) . (\dfrac{1}{R_1} + \dfrac{1}{R_2}) }\) |
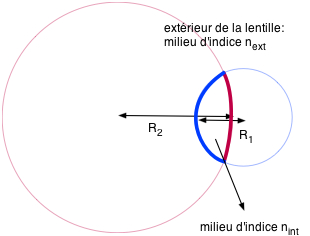 |
*  voir note sur les signes
voir note sur les signes
u et v sont parfois notés p et q.
A la place de I et O, on utilise parfois yI et yO. Ces grandeurs sont positives si au-dessus de l'axe optique, négatives en-dessous. Dans ce cas, au lieu de G, on utilise m (ou g) : \( \class{formule}{ m = \dfrac{y_I}{y_O} = - \dfrac{q}{p} }\).
Conventions de signes
 Sur ce site, nous avons fait le choix d'utiliser une seule équation: \( \class{formule}{ \dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v} }\), quel que soit le type de lentille, d'objet et d'image.
Sur ce site, nous avons fait le choix d'utiliser une seule équation: \( \class{formule}{ \dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v} }\), quel que soit le type de lentille, d'objet et d'image.
Dans ce cas, f u et v sont des grandeurs positives ou négatives (voir le tableau des signes ci-dessous).
Parfois, on trouve une autre approche, celle d'avoir une formule différente pour chaque cas, mais alors, f, u et v sont des grandeurs toujours positives.
Notre approche est plus facile à appliquer lorsque l'une ou l'autre de ces grandeurs est inconnue, d'où le choix fait pour ce site.
R > 0 ⇒ face convexe, R < 0 ⇒ face concave
f > 0 ⇒ convergente, f < 0 ⇒ divergente
u > 0 ⇒ objet réel, u < 0 ⇒ objet virtuel
v > 0 ⇒ image réelle, v < 0 ⇒ image virtuelle
\( \class{formule}{ \dfrac{v}{u} > 0 }\) ⇒ image renversée, \( \class{formule}{ \dfrac{v}{u} < 0 }\) ⇒ image droite
Construction
| rayon incident | rayon réfracté après la lentille |
|---|---|
| 1. par le foyer | parallèle à l'axe optique |
| 2. parallèle à l'axe optique | par le foyer |
| 3. par le centre optique | pas dévié |
Schémas (cliquez sur les icônes pour les agrandir)
| lentille convergente | lentille divergente |
|---|---|
 |
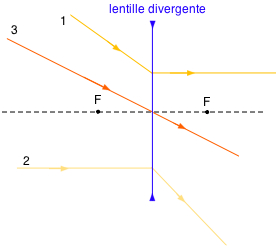 |
Vergence
= inverse de la distance focale \( \class{formule}{ \class{symbol}{V} = \dfrac{1}{f} }\)
Unité : la dioptrie = 1/mètre
Association de lentilles minces accolées
lentilles minces accolées : \( \class{formule}{ \dfrac{1}{f} = \dfrac{1}{f_1} + \dfrac{1}{f_2} }\)






