Réflexion
- prérequis
- lois de la réflexion
- image d'un objet
- miroirs courbes
- conventions de signe
- construction du rayon réfléchi
Prérequis
aucun
Lois de la réflexion
|
1) rayon incident, normale et rayon réfléchi dans un même plan 2) i = r (mais de l'autre côté de la normale) |
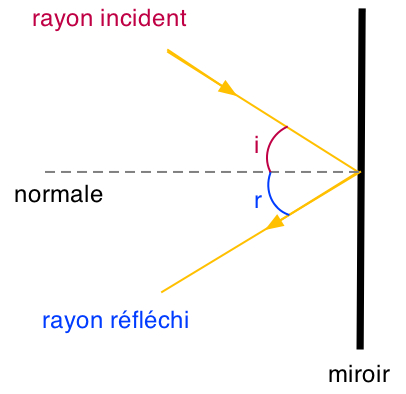 |
Note importante : dans ce cours, les angles sont mesurés par rapport à la normale (voir schéma ci-dessus).
Image d'un objet
Vision directe, image réelle, image virtuelle : voir ici
Construction de l'image d'un objet
Si l'objet est sur l'axe principal, cherchez l'image de son autre extrémité. Pour cela, faites la construction géométrique pour deux rayons lumineux particuliers (voir ici).
Là où les rayons réfléchis se croisent se trouve l'image réelle de ce point. Si ces rayons divergent, leurs prolongements se croisent; à cet endroit se trouve l'image virtuelle du point.
Miroirs courbes : 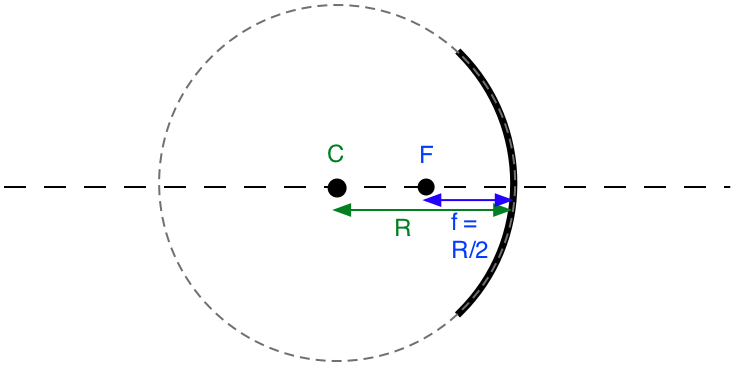
\( \class{formule}{ f = \dfrac{R}{2} }\) \( \class{formule}{ \dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v} }\) * \( \class{formule}{ G = \dfrac{I}{O} = \dfrac{|v|}{|u|} }\) |
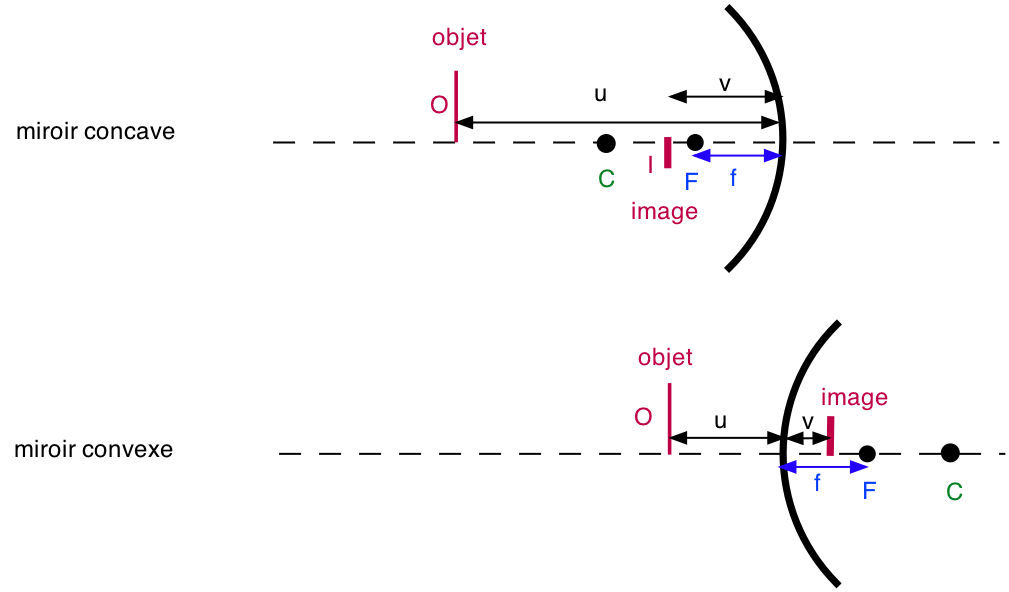 |
*  voir note sur les signes
voir note sur les signes
u et v sont parfois notés p et q.
A la place de I et O, on utilise parfois yI et yO. Ces grandeurs sont positives si au-dessus de l'axe optique, négatives en-dessous. Dans ce cas, au lieu de G, on utilise m (ou g) : \( \class{formule}{ m = \dfrac{y_I}{y_O} = - \dfrac{q}{p} }\).
Conventions de signe
 Sur ce site, nous avons fait le choix d'utiliser une seule équation:
\( \class{formule}{ \dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v} }\), quel que soit le type de miroir, d'objet et d'image.
Sur ce site, nous avons fait le choix d'utiliser une seule équation:
\( \class{formule}{ \dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v} }\), quel que soit le type de miroir, d'objet et d'image.
Dans ce cas, f u et v sont des grandeurs positives ou négatives (voir les signes dans le tableau ci-dessous).
Parfois, on trouve une autre approche, celle d'avoir une formule différente pour chaque cas, mais alors, f, u et v sont des grandeurs toujours positives.
Notre approche est plus facile à appliquer lorsque l'une ou l'autre de ces grandeurs est inconnue, d'où le choix fait pour ce site.
| f > 0 ⇒ miroir concave | f < 0 ⇒ miroir convexe |
| u > 0 ⇒ objet réel | u < 0 ⇒ objet virtuel |
| v > 0 ⇒ image réelle | v < 0 ⇒ image virtuelle |
| \( \class{formule}{ \dfrac{v}{u} > 0 }\) ⇒ image renversée | \( \class{formule}{ \dfrac{v}{u} < 0 }\) ⇒ image droite |
Construction du rayon réfléchi
Pour un miroir plan, utilisez les lois de la réflexion.
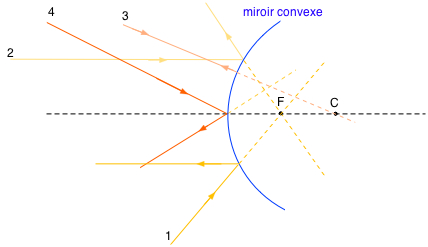
Pour un miroir courbe, voici quelques rayons particuliers:
| rayon incident | rayon réfléchi |
|---|---|
| 1. par le foyer | parallèle à l'axe optique |
| 2. parallèle à l'axe optique | par le foyer |
| 3. par le centre de courbure | sur lui-même |
| 4. par le centre du miroir | symétrique par rapport à l'axe optique (i = f) |
schémas (cliquez sur les icônes pour les agrandir):
| miroir concave | miroir convexe |
|---|---|
 |
 |






