Déformations des solides
Prérequis
- la dynamique du point présentée sur ce site,
- la dynamique du solide (pour les moments de force)
Les 3 domaines des déformations
Selon le matériau, la force exercée et le type de déformation, on peut avoir :
- déformation élastique,
- déformation plastique,
- rupture.
Les 3 types de déformations 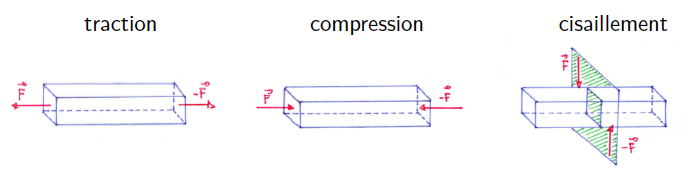
- traction (2 forces de même direction, sur la même droite, et de sens opposé, entrainant une augmentation de la longueur)
- compression (2 forces de même direction, sur la même droite, et de sens opposé, entrainant une diminution de la longueur)
- dont compression en volume (dans les 3 directions) schéma,
- flambage (force dans la direction de la longueur entrainant une déformation dans une autre direction, provoquant une flexion du corps puis la rupture) schéma
- cisaillement (2 forces tangentielles de même direction, sur des droites différentes, et de sens opposé)
Quelques relations utiles
Loi de Hooke (déformations élastiques)
La loi de Hooke donne la relation entre
- la cause (la contrainte)
- et l'effet (la déformation).
| traction | \( \class{formule}{ ε_l = \dfrac{Δl}{l_0} = \dfrac{1}{E} . \dfrac{F}{S_0} }\) et dans le plan transversal, \( \class{formule}{ ε_t = - \dfrac{1}{ν} . ε_l }\) |
où E = module d'élasticité ou module de Young ν est le coefficient de Poisson |
| compression linéaire | \( \class{formule}{ \dfrac{Δl}{l_0} = \dfrac{-1}{K} . \dfrac{F}{S_0} }\) | où K = module de compressibilité |
| compression en volume | \( \class{formule}{ \dfrac{ΔV}{V_0} = \dfrac{-1}{B} . \dfrac{F}{S_0} }\) | où B = module de compressibilité en volume (Bulk, aussi noté Ep) schéma |
| cisaillement | \( \class{formule}{ α ≅ \dfrac{Δd}{l_0} = \dfrac{1}{η} . \dfrac{F}{S_0} }\) | où η = module de cisaillement ou
de rigidité (aussi noté G), α = l'angle de cisaillement schéma |
| torsion | \( \class{formule}{ θ = \dfrac{1}{η} . \dfrac{L}{r} . \dfrac{dF}{dS} }\) | où η = module de rigidité, θ = l'angle de torsion schéma |
Liens entre ces modules
K ≅ E pour des solides simples, mais K ≠ E pour des structures complexes (tissus biologiques)
\( \class{formule}{ B = \dfrac{E}{3 . (1 - 2 . ν)} }\)
\( \class{formule}{ η = \dfrac{E}{2 . (1 + ν)} }\)
Flexion
\( \class{formule}{ M = E . \dfrac{J}{R} }\) (= formule de flexion) schéma
- où J (parfois noté IS) = moment d'inertie de la section droite ou moment quadratique \( \class{formule}{ = \int_{-a/2}^{+a/2} x^2 . dS }\)
avec x = distance à la ligne neutre et a = épaisseur du solide, (à ne pas confondre avec le moment d'inertie I), - R = rayon de courbure
Torsion
Couple de forces de torsion ⇒ moment de torsion :
\( \class{formule}{ M = η . θ . \dfrac{I_p}{L} }\) où Ip est le moment polaire de la section = ∫ r2 . dS et vaut π . r4 / 2 pour une section circulaire
On peut la réécrire comme M = k . θ où k = coefficient de torsion
Pour un cylindre plein (p. ex. un fil), \( \class{formule}{ k = \dfrac{π . η . r^4}{2 . L} }\)






