Statique - biomécanique

Ceci est un complément du rappel de statique dans la dynamique du solide.

Ces deux équations sont appelées les conditions d'équilibre.

Quelques outils supplémentaires

Calcul du centre des forces d'un ensemble de forces parallèles ou antiparallèles (norme F_i, position du point d'application r_i par rapport à un point quelconque) :

\( \class{formule}{ \class{symbol} {\vec{R}} = \dfrac{\sum F_i . \vec{r}_i }{ \sum F_i} + n . \vec{u}_t }\)

où n est un nombre quelconque et u_t un vecteur unitaire dans la direction des forces.
Ce centre est donc en n'importe quel point d'une droite parallèle aux forces.

Intérêt

Pour équilibrer l'objet, il suffit d'appliquer en ce point une force supplémentaire égale à la résultante des forces mais de sens opposé, car alors les deux conditions d'équilibre de la statique (∑ £F = £0 et ∑ £M = £0) sont vérifiées.

Application au centre de gravité

\( \class{formule}{ \vec{R} = \dfrac{\int \vec{r} . g(\vec{r}) . ρ . dV}{F_G} }\) ( \( \class{formule} { = \dfrac{\sum \vec{r}_i . g(\vec{r}_i) . m_i}{F_G} }\) pour un ensemble discret)
Si l'objet est de petite taille (g cst) alors \( \class{formule}{ \vec{R} = \dfrac{\int \vec{r} . ρ . dV}{M} }\) ( \( \class{formule} { = \dfrac{\sum \vec{r}_i . m_i}{M} }\) pour un ensemble discret), et le centre de gravité se confond avec le centre de masse.

Equilibre

Un corps est à l'équilibre si son centre de gravité est à la verticale du point (ou de la zone) d'appui sur le sol.

On peut avoir un équilibre

• stable (lors d'un léger écart, le moment de P ramène l'objet à sa position d'équilibre),
• instable (le moment de P éloigne encore plus l'objet de sa position d'équilibre) ou
• indifférent (changement léger de la position d'équilibre).

Classes de leviers

Soient deux forces appliquées au levier (en supposant que le poids du levier soit négligeable) :

• £F_R force de résistance à vaincre (souvent le poids),
• £F_A force motrice appliquée (force musculaire en anatomie)

classe	position du point d'appui	forces (sauf R) vers le bas	forces (sauf R) vers le haut	schéma
1 levier inter-appui	centrale	les deux, de part et d'autre du point d'appui	/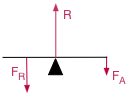
2 levier inter-résistant	à une extrémité du levier	une, en un point intermédiaire du levier	une, à l'autre extrémité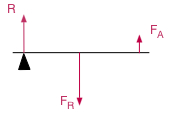
3 levier inter-effort	à une extrémité du levier, attaché à celui-ci, ou avec le point d'appui au-dessus.	une, à l'autre extrémité	une, en un point intermédiaire du levier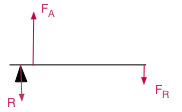

Avantage mécanique : \( \class{formule}{ \class{symbol} {AM} = \dfrac{F_R}{F_A} = \dfrac{x_A}{x_R} = \dfrac{v_A}{v_R} }\) (x = bras de levier, v = vitesse)

En utilisation normale,

• les classes 2 sont des multiplicateurs de force (AM > 1),
• les classes 3 sont des multiplicateurs de vitesse (AM < 1),
• tandis que les classes 1 peuvent fonctionner des deux façons.

Observez ici des schémas de 3 applications en anatomie (biomécanique).

Dans la pratique, on devra tenir compte du poids du levier, il peut y avoir plus de forces, et celles-ci ne sont pas nécessairement perpendiculaires au levier.

Que cela ne vous perturbe pas; il suffit d'appliquer ∑ £F = £0 et ∑ £M = £0