Courant alternatif - la représentation de Fresnel
Prérequis
Présentation
Animation pour illustrer la représentation de Fresnel du courant alternatif ou de la tension alternative.
auteur : Geneviève Tulloue, université de Nantes
Explications
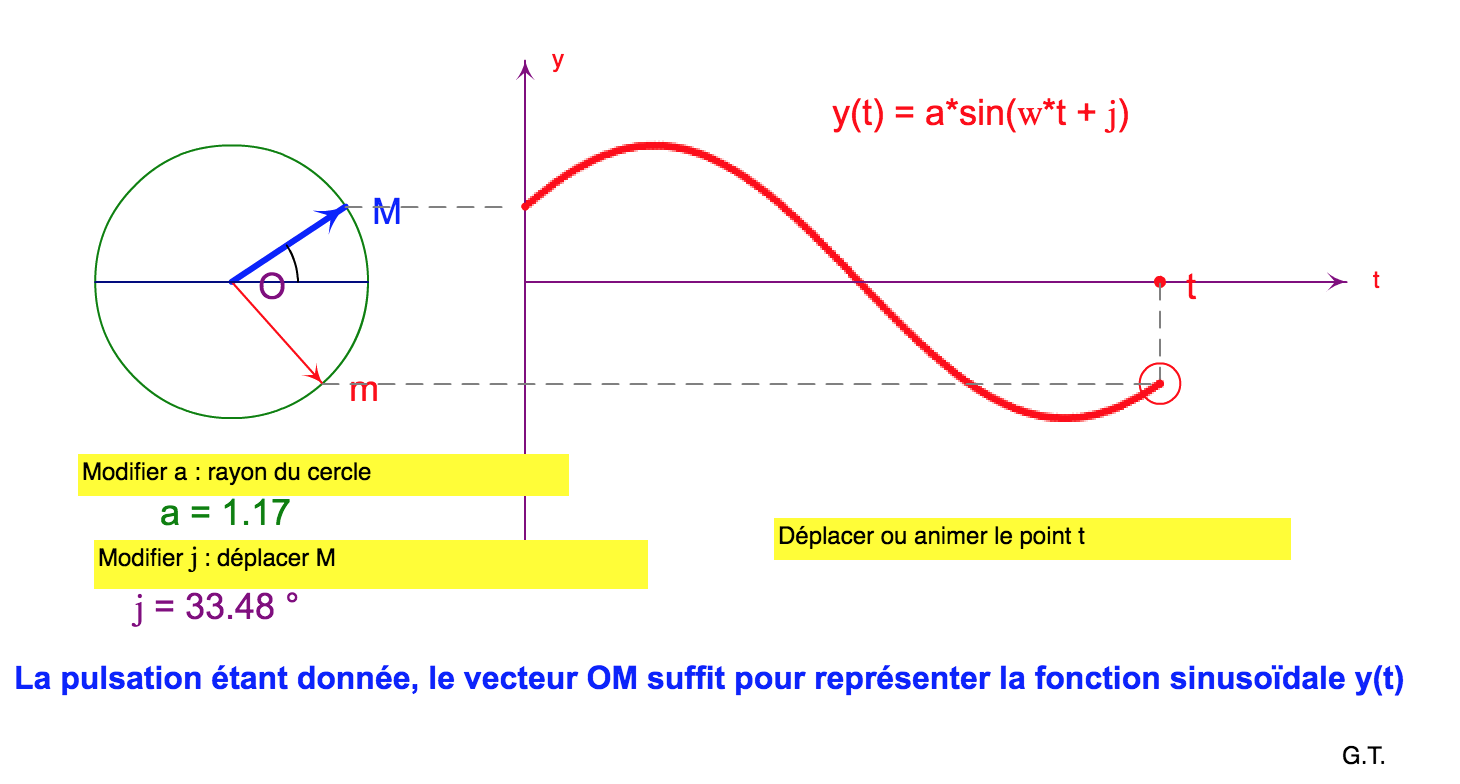
Le courant alternatif varie de façon sinusoïdale : i = Im . sin(ω . t + φ) (graphe dans la partie droite du cadre).
On peut représenter ce courant par un vecteur tournant de longueur Im dont la projeter sur l'axe vertical est la valeur instantanée.
Ce vecteur tourne avec une vitesse angulaire ω, appelée pulsation, et à t = 0, il fait déjà un angle φ avec l'axe horizontal, appelé constante de phase (partie gauche du cadre).
Vous pouvez arrêter l'animation en cliquant une fois dessus et la redémarrer de la même manière. Ceci vous permet de faire du pas par pas pour bien voir le lien entre la position du vecteur tournant et le point dans le graphique de i(t).
Modifiez les paramètres suivants et observez ce que cela change :
- la valeur maximum, en tirant sur le bord du cercle,
- la constante de phase, en faisant tourner le bout du vecteur tournant. Essayez une constante de phase négative (en-dessous de l'axe horizontal).