-
Calcul du champ
|
On procède par addition des champs H créés par chacune des m bobines. |
Le champ H est encore une fonction paire. |
|
- Calcul des harmoniques d'espace
|
|
Pour calculer les harmoniques d'espace, on procède par addition des harmoniques de même rang des champs créés par chacun des enroulements.
D'une façon générale, comme le champ H est encore une fonction paire, l'harmonique d'espace de rang n du champ créé par l'ensemble des m bobines est égal à :
avec 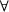 i : i :
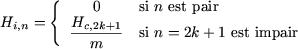
où :
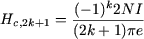
représente le coefficient de l'harmonique de rang 2k+1 du champ que créeraient les N spires de l'enroulement si elles étaient concentrées dans deux encoches diamétralement opposées.
Construction géométrique du coefficient Hn
La construction géométrique qui permet de déterminer la valeur des coefficients Hn des harmoniques impaires est similaire à celle utilisée dans le cas où il y avait seulement deux bobines. Elle se base également sur la valeur de l'expression (1) calculée pour q = 0. |
|
|
On en déduit que les coefficients Hn des harmoniques de rang impair s'écrivent :
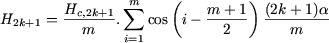
|
(2) |
|
- Dans le cas particulier où m = 3, on a ainsi :
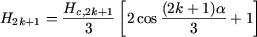
- H3 s'annule pour : cos
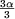 = - = - 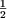 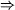 a = a = 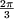 soit a = 120° soit a = 120°
- H5 s'annule pour : cos
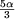 = - = - 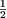 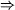 a = a = 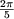 soit a = 72° soit a = 72°
|
|
- Dans le cas particulier où m = 4, on a :
On vérifie, une fois de plus, que l'harmonique de rang 3 s'annule pour a = 120° tandis que celle de rang 5 s'annule pour a = 72° . |
|
| On peut étendre ce résultat à un nombre m quelconque de bobines. La somme (2) peut en effet être évaluée en considérant sa représentation géométrique.
H2k+1 est ainsi représenté sur la figure 1, par le vecteur 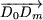 , somme des vecteurs , somme des vecteurs 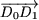 , , 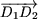 ,..., ,..., 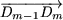 , ,
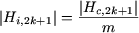
- déphasés les uns par rapport aux autres d'un angle n.b =
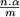 . .
|
|
|
|
|
|
Les points D0 à Dm s'inscrivent sur un cercle de centre O et de rayon OD0 (figure 2). Les points O,Di-1,Di, i = 1,2,¼,m forment un triangle isocèle, d'angle g à la base et d au sommet. On montre aisément (cf. figure 2) que 2g+n.b = p.
Comme de plus la somme des angles d'un triangle est égale à p, on en déduit que 2g+d = p d'où finalement d = n.b. |
|
|
|
|
|
La longueur du rayon OD0 est alors donnée par (cf. figure 3):
et la valeur de la corde D0Dm, par :
On en déduit finalement :
soit encore, exprimé en fonction de l'angle d'étalement a :
|
|
|
|
|
|
On vérifie ainsi que, "m, l'harmonique de rang 3 s'annule pour sin 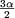 = 0 soit a = 120°, tandis que celui de rang 5 s'annule pour a = 72° = 0 soit a = 120°, tandis que celui de rang 5 s'annule pour a = 72° |
|