Question 4.a :

Deux approches sont possibles pour le calcul de H :

1. soit procéder comme précédemment, à savoir appliquer le théorème d'Ampère à des contours bien choisis pour calculer H en tout point ;
2. soit considérer que le champ H créé par ces deux bobines peut-être calculé comme la somme des champs créé par chacune d'entre elles.

1. Application du théorème d'Ampère

Deux types de contours peuvent être envisagés :

Le premier entoure deux encoches parcourues des courants de même signe (cf Figure 1). Par application du théorème d'Ampère, on calcule :

Figure 1

Comme :

• H est nul dans le fer et radial dans l'entrefer ;
• par raison de symétrie, H(q ) = -H( p-q )

on obtient :   

soit encore :

Figure 2

On en conclut que :

Le champ H est encore une fonction paire.

2. Somme des champs créés par chacune des bobines

On peut calculer le champ total créé par les deux bobines en additionnant le champ chacune d'entre elles. La première crée, en tout point de l'entrefer un champ déphasé de -, la seconde un champ déphasé de +.

Question 4.b :

Là encore deux approches sont possibles :

1. soit le calcul direct
2. soit l' addition des composantes harmoniques des champs créés par chacune des bobines

1. Calcul direct

De même que précédemment, on calcule, compte-tenu de la forme du champ :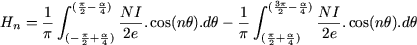

Deux cas se présentent encore :

• soit n est pair (n = 2k) et alors la fonction cos(2kq) a une périodicité de . L'intégrale de cette fonction calculée entre (- +) et ( -) est donc égale à celle calculée entre ( + ) et ( - ).

  On en déduit que les harmoniques de rang pair sont nuls.

• soit n est impair (n = 2k + 1) et alors :

2. Addition des composantes harmoniques des champs créés par chacune des bobines

L'harmonique de rang n du champ créé par deux bobines est égal à la somme des harmoniques de même rang des champs créés par chacune des deux bobines; comme le champ H est une fonction paire, on a :

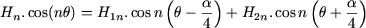
où (pour i = 1 ou i = 2) :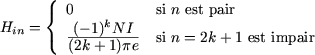

On en déduit immédiatement que les harmoniques H_n de rang pairs sont nuls.

Comme pour q = 0, on a :

(équation 1)

On en déduit que les coefficients de Fourier des harmoniques de rang impairs sont égaux à :