On a vu précédemment que le champ H(q) crée par une spire parcourue par un courant I était une fonction paire de la variable q, de période 2p (cf. Figure 1). Dans ces conditions, l'harmonique de rang n de H s'écrit Hn cos(nq), avec :
|
|

|
figure 1 |
Deux cas se présentent alors : soit n est pair (n = 2k) et alors : 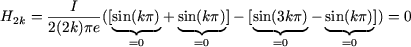
Les coefficients de Fourier des harmoniques de rangs pairs sont nuls. Ces harmoniques n'existent pas. soit n est impair (n = 2k + 1) et alors : 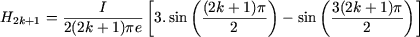
Les coefficients de Fourier des harmoniques de rangs impairs sont égaux à : 
On a :
|