Dérivées et différentielles - accroissement et différentielle

Prérequis

• les fonctions
• les dérivées
• les différentielles

Présentation

Dans la vidéo, vous voyez

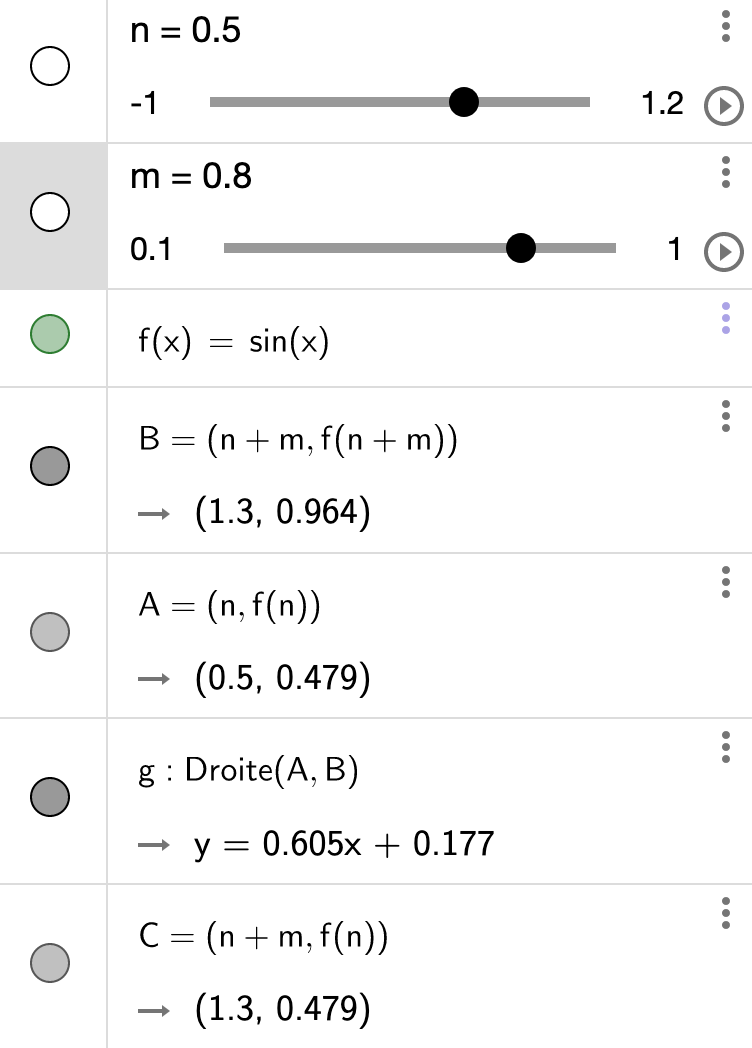
• une fonction f(x), ici la fonction sinus,
• deux points A et B sur la courbe,
• une droite passant par A et B.
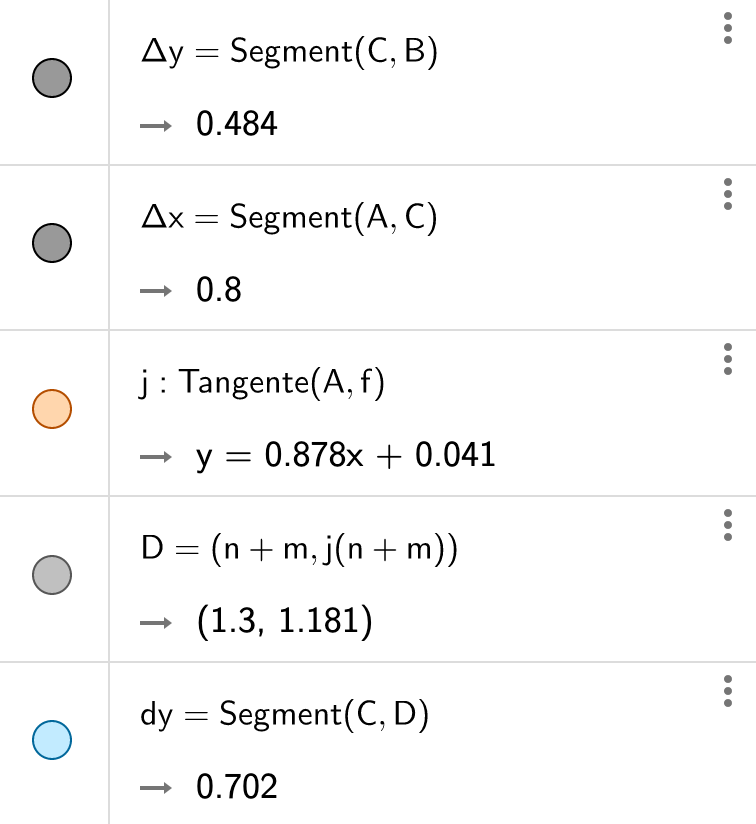
• Pour aller de A à B, il y a un accroissement Δx et un accroissement Δy
• On trace la tangente à la courbe f(x) en A. La différentielle dy est le segment vertical qui va du point de coordonnées (B_x,A_y) jusqu'à la tangente.
• Lorsqu'on diminue l'accroissement Δx, on voit que la différence entre cette différentielle dy et l'accroissement Δy est de plus en plus petite. C'est pour cela que calculer la différentielle à la place de l'accroissement (calcul souvent plus long) constitue une bonne approximation.

Pour construire vous-même une autre fonction, et/ou chercher la différentielle en un autre point, utilisez GeoGebra (application ou version en ligne), en vous inspirant des éléments ci-dessous.