Superposition de mouvements oscillatoires harmoniques

• prérequis
• général
• deux cas particuliers

Prérequis

• mathématiques :
  • trigonométrie,
  • vecteurs,
• mouvements oscillatoires harmoniques.

Mouvement oscillatoire résultant

φ = phase = angle dont on calcule le cosinus = ω . t + ε
Δφ = déphasage ou différence de phase = φ₁ - φ₂

Si les 2 vibrations qui se superposent ont la même direction, l'amplitude du mouvement oscillatoire résultant vaut :

A² = A₁² + A₂² + 2 . A₁ . A₂ cos Δφ

Deux cas particuliers

1. même fréquence

⇒ Δφ = Δε

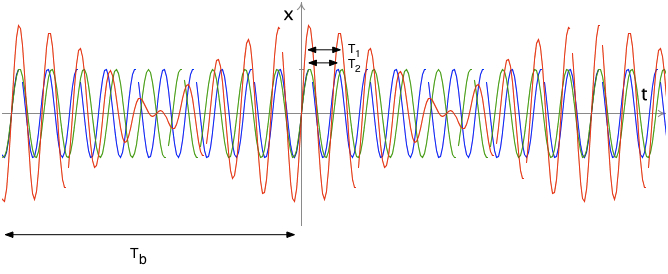
2. fréquences proches

⇒ battements :

Dans le dessin ci-dessous, on a pris le cas particulier où A₁ = A₂.

\( \class{formule}{ f_1 = \dfrac{1}{T_1} }\), \( \class{formule}{ f_2 = \dfrac{1}{T_2} }\)
\( \class{formule}{ f_b = \dfrac{1}{T_b} }\); T_b est appelée la période de battement.