Fonctions - les logarithmes
Prérequis
Définition et graphes
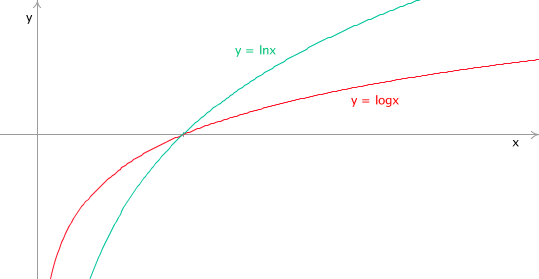
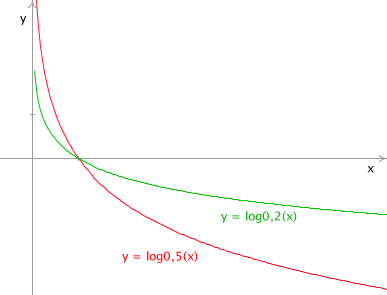
La fonction logarithme est la fonction y = f(x) = logax
| base > 1 | base < 1 |
|
 |
Papier semi-log et log-log
Il existe des papiers spéciaux avec les axes gradués selon des échelles non linéaires pour représenter des logarithmes sans devoir les calculer :
- le papier semi-logarithmique
- une échelle linéaire et une échelle logarithmique;
- on l'utilise pour représenter des fonctions de type y = A . exp(-t/τ),
- car ln y = ln A - t/τ est l'équation d'une droite.
- A est l'ordonnée à l'origine de cette droite, et -1/τ est sa pente \( \class{formule}{ = \dfrac{ln y_2 - ln y_1}{x_2 - x_1} }\)
- le papier log-log
- les 2 échelles logarithmiques;
- on l'utilise pour représenter des fonctions de type y = a . xb,
- car ln y = ln a + b . ln x est l'équation d'une droite.
- a est son ordonnée à l'origine, et b est sa pente \( \class{formule}{ = \dfrac{ln y_2 - ln y_1}{ln x_2 - ln x_1} }\)
Ci-dessous un petit morceau de papier semi-logarithmique, à gauche et de papier log-log à droite.