Erreurs (incertitudes) de mesure
- prérequis
- erreur (incertitude) absolue
- erreur (incertitude) relative
- erreur (incertitude) sur une fonction de plusieurs variables
- erreur statistique
Prérequis
Erreur (incertitude) absolue
Lors de la mesure d'une grandeur physique,
la valeur réelle de la grandeur ainsi que l'erreur commise sont inconnues.
On ne détermine qu'une estimation de l'erreur, et plus exactement une limite supérieure, qu'on appelle "erreur absolue".
C'est parce qu'on ne connait que cette estimation de l'erreur qu'on l'appelle parfois "incertitude".
grandeur x → erreur (ou incertitude) absolue : E.A. = Δx
Soit x0 la valeur réelle et xm la valeur mesurée, x0 ∈ [xm - Δx ; xm + Δx]
Erreur (ou incertitude) relative
Elle permet de mieux se rendre compte de l'importance de l'incertitude.
\( \class{formule}{E.R. = \dfrac{Δx}{x} }\)
Elle peut être exprimée telle quelle ou en pourcents : \( \class{formule}{E.R.(\%) = (\dfrac{Δx}{x}) . 100 \% }\)
Erreur sur une fonction de plusieurs grandeurs
Considérons maintenant une fonction f de plusieurs variables x1, x2, ...
Soit
| xi, | des mesures de variables indépendantes, |
| Δxi | les incertitudes de mesure sur ces grandeurs, |
| f | qui est fonction de ces variables. |
⇒ erreur (incertitude) absolue \( \class{formule}{ Δf = ∑ | \dfrac{∂f}{∂x_i} | . Δx_i }\)
Remarquez qu'il s'agit d'une application des différentielles MAIS que les dérivées partielles sont prises en valeur absolue.
Erreurs (incertitudes) statistiques
On peut aussi estimer la valeur d'une grandeur physique de façon plus fine, en prenant un grand nombre de mesures.
Soit une grandeur physique y. Soit n mesures de cette grandeur y1, y2, ..., yn.
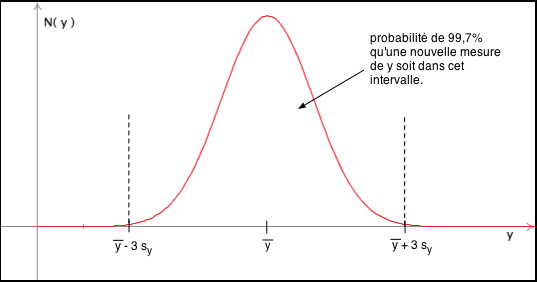
Ces valeurs se répartissent selon une distribution gaussienne, centrée sur la valeur moyenne, symétrique, avec l'axe des y comme asymptote horizontale.
- On estime la valeur réelle (inconnue) de y par la moyenne arithmétique des mesures : \( \class{formule}{ \overline{y} = \dfrac{∑y_i}{n} }\)
- La dispersion des résultats est estimée par l'écart-type expérimental : \( \class{formule}{ s_y = \sqrt{\dfrac{∑(y_i - \overline{y})^2}{n-1} } }\).
Si on prend une mesure supplémentaire, il y a 99,7 % de chances qu'elle tombe dans l'intervalle [y - 3 sy ; y + 3 sy].
Dès lors, dans un calcul d'incertitude, il est raisonnable de prendre 3. sy comme estimation de l'erreur absolue, même si cela ne constitue pas à strictement parler d'une borne supérieure de l'erreur commise.
Si on prend un nouvel échantillon, la moyenne sera différente.
Les moyennes d'un grand nombre d'échantillons se répartissent aussi selon une gaussienne, dont l'écart-type vaut \( \class{formule}{ s_m = \dfrac{s_y }{ \sqrt{n}} }\).
La valeur moyenne calculée sur un échantillon a 99,7 % de chances de tomber dans l'intervalle [y - 3 sm ; y + 3 sm].






