Fonctions - fonctions exponentielles

Prérequis

• les fonctions
• les exponentielles

Présentation

Dans cette vidéo, vous voyez une fonction exponentielle y = exp(n.x) = e^(n.x).

1. Dans un premier temps n est positif. Observez l'allure de la courbe. Observez comment elle varie quand n augmente ou diminue. Observez l'intersection de cette courbe avec l'axe Y.
   Ensuite, on trace une tangente à la courbe, en un point qu'on peut déplacer. Comment varie cette droite quand n varie ? Est-elle croissante ou décroissante ?

2. Dans un second temps, n est négatif. Qu'est-ce que cela change ?
   A nouveau, observez comment la courbe varie quand n augmente ou diminue. Observez l'intersection de cette courbe avec l'axe Y.
   Ensuite, on trace une tangente à la courbe, en un point qu'on peut déplacer. Comment varie cette droite quand n varie ? Est-elle croissante ou décroissante ?

   Pour l'exponentielle à coefficient négatif, on peut trouver la valeur de n en observant la courbe.
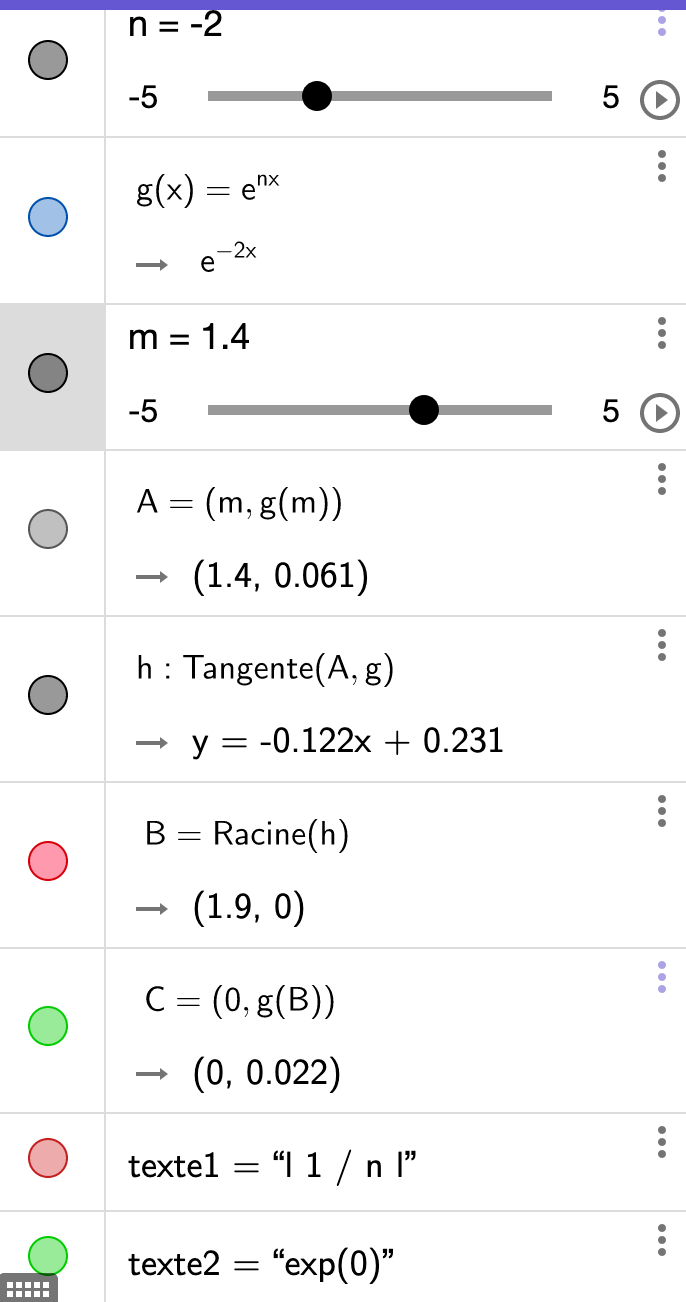
   Deux méthodes pour cela.

   1. On trace la tangente à la courbe au point d'intersection avec l'axe Y. Cette droite coupe l'axe X en un point B. L'abscisse de B (B_x) vaut | 1/n |. Observez comment ce point B varie quand n varie.
   2. Observez la valeur de e^n.B_x. Comment varie-t-elle quand n varie ? On voit que ... elle est constante et vaut 0,37, qui est l'exponentielle de 0. Donc pour trouver la valeur de n, on peut chercher le point C de coordonnées (0, 0,37) et ensuite chercher le point B correspondant.

Pour construire vous-même cette fonction pour l'animer vous-même, utilisez GeoGebra (application ou version en ligne), en vous inspirant des éléments indiqués ci-dessous.

Test Geogebra interactif