Vecteurs - composantes et addition
Prérequis
Présentation
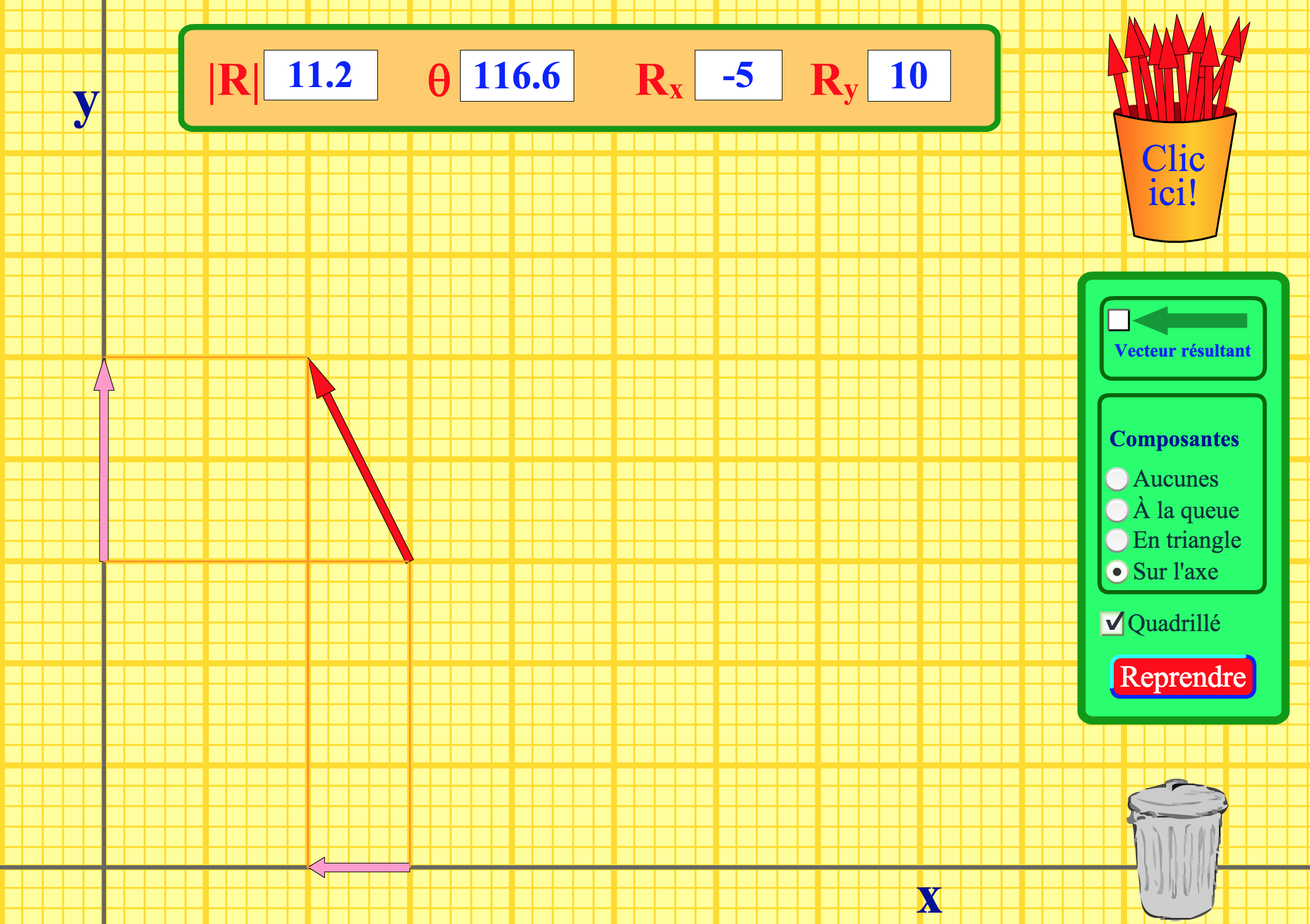
Cochez les cases "Composantes sur l'axe" et "Quadrillé".
- Prenez un vecteur. Faites-le tourner lentement pour lui faire décrire tout un tour. Observez comment varient les composantes selon les 2 axes, sur le dessin mais aussi les valeurs.
- Donnez-lui une certaine orientation dans l'espace. Calculez puis vérifier les valeurs de ses composantes.
- Changez son orientation et faites la démarche inverse: à partir des composantes, calculez la norme et l'angle avec l'axe X, puis vérifiez.
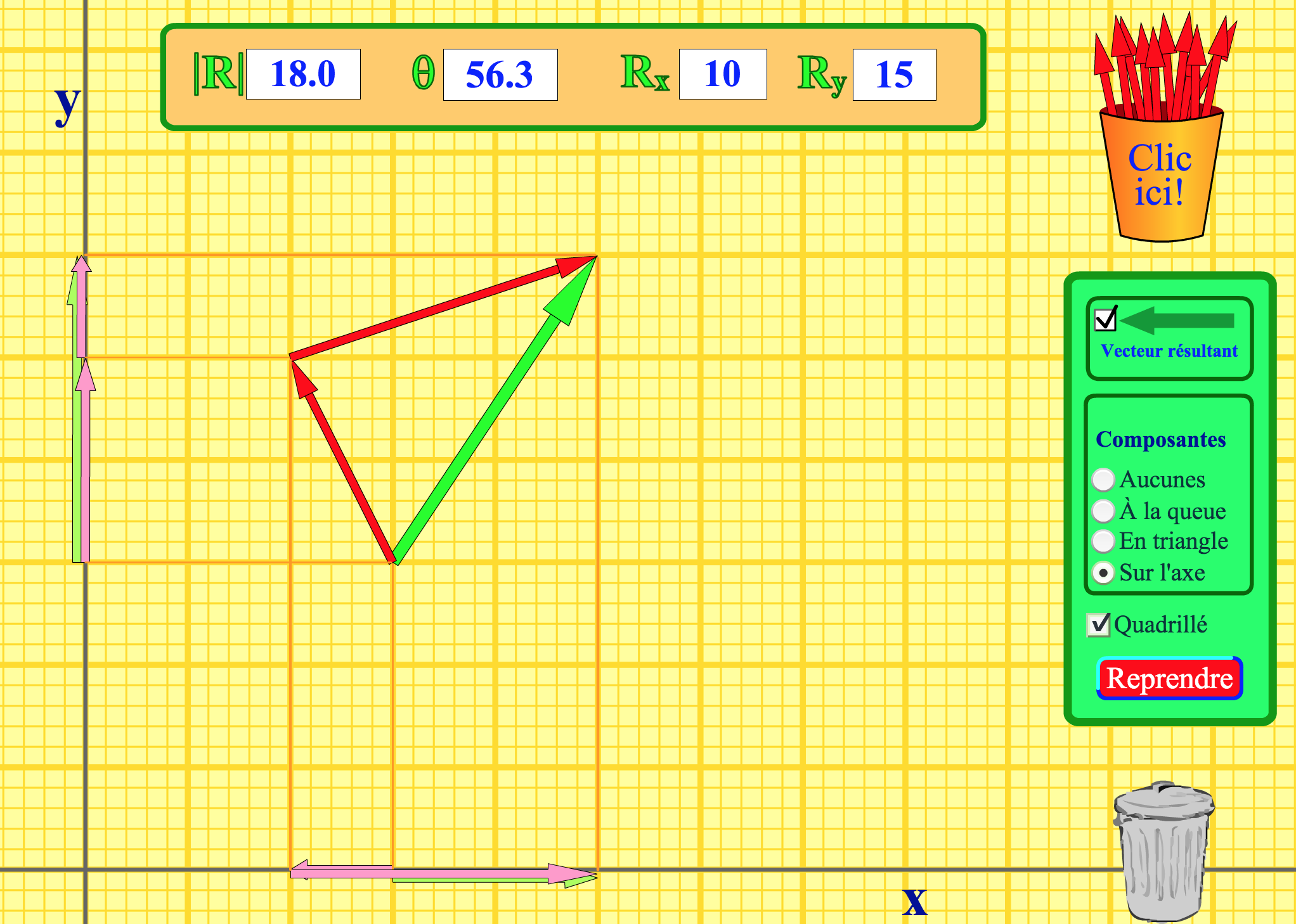
- Ajoutez un second vecteur, de sorte que son origine coïncinde avec l'extrémité du premier. Cochez la case "Vecteur résultant". Placez cette résultante de façon à ce que son origine coïncinde avec celle du premier vecteur. Observez la construction, mais aussi ce qui se passe avec les composantes.
- Cliquez sur chacun des vecteurs rouges et notez leur norme, leur angle avec X et leurs composantes. Calculez les composantes de la résultante, puis, à partir de ces composantes, sa norme et son angle avec X. Cliquez sur le vecteur résultante et regardez si vos calculs sont exacts.
- Refaites le calcul de la norme de la résultante en utilisant la formule R = √(R12 + R22 + 2 . R1 . R2 . cosα) où α est l'angle entre les deux vecteurs (à calculer). Obtenez-vous la bonne réponse ?
- Refaites ces manipulations et calculs pour une autre orientation des vecteurs rouges (par exemple, l'un d'eux dirigé vers le bas ou vers la gauche).
auteur: Simulations interactives PhET à l'Université du Colorado Boulder