Dérivées - accroissement et dérivée

Prérequis

• les fonctions
• les dérivées

Présentation

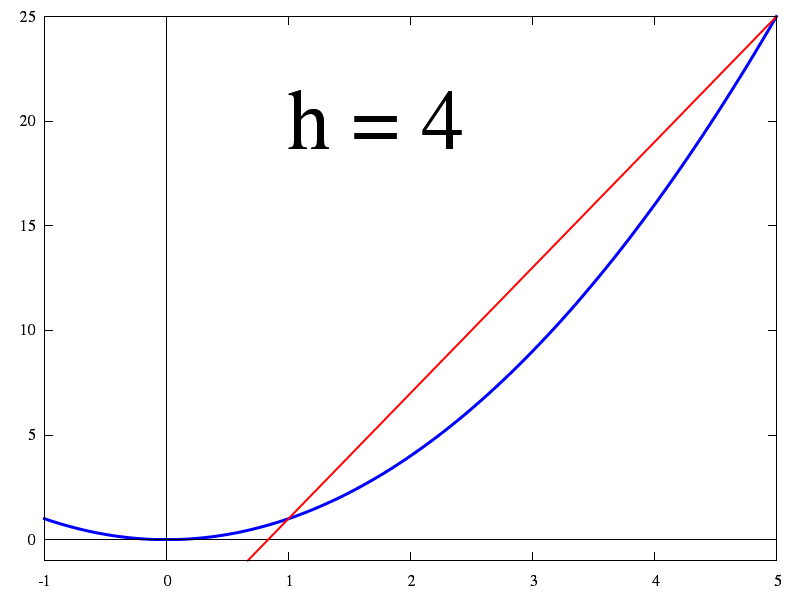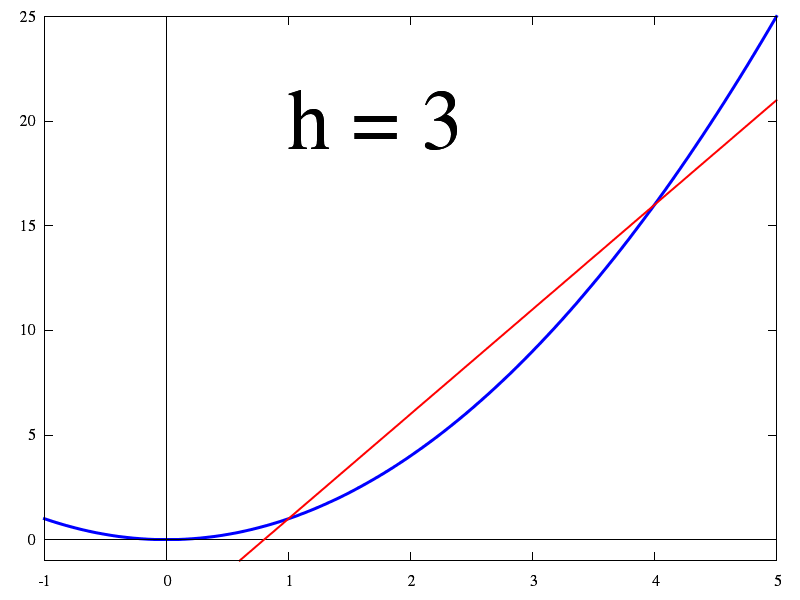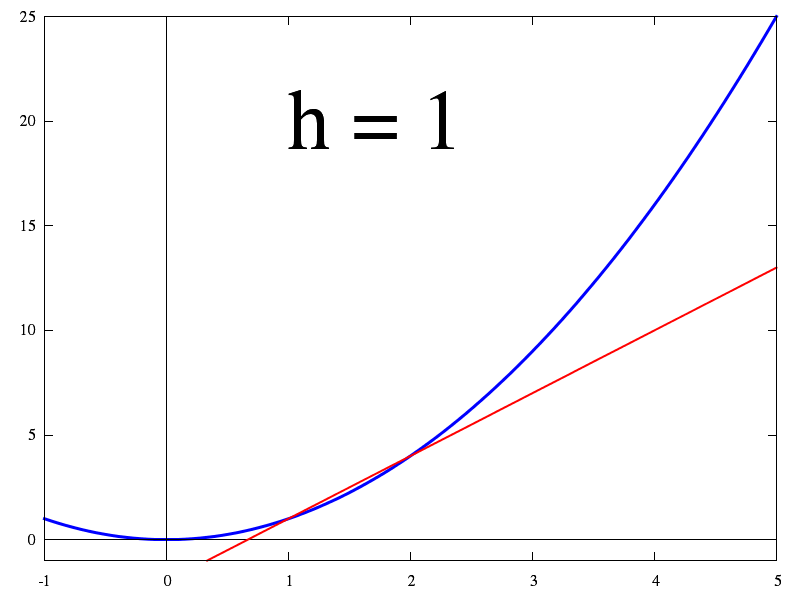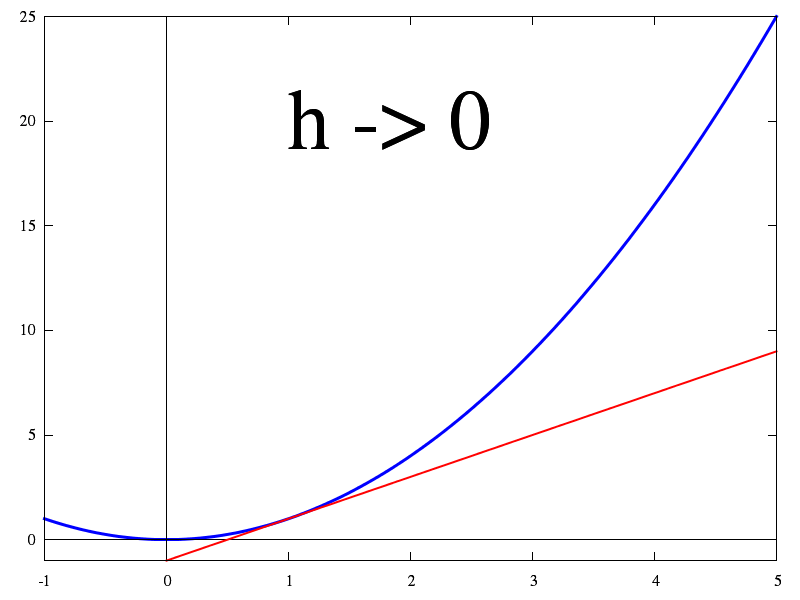
Cette première animation montre le passage de l'accroissement à la dérivée.
Le h représente ce qu'on a nommé Δx ailleurs sur ce site.
Lorsque h tend vers 0, l'accroissement tend vers la dérivée (= définition de la dérivée).

Par IkamusumeFan (Travail personnel) [CC BY-SA 3.0], via Wikimedia Commons

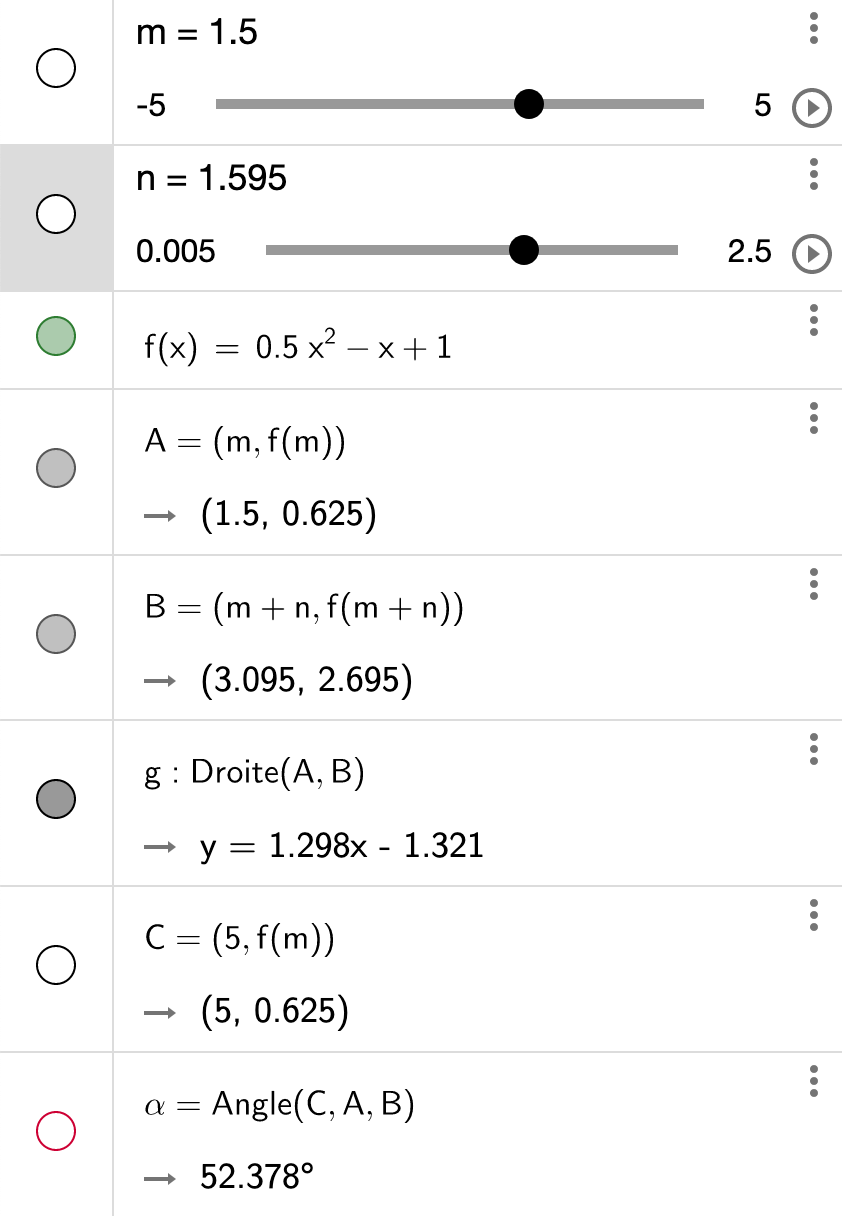
Dans la vidéo ci-dessous, vous voyez

• une fonction f(x), ici une parabole,
• deux points A et B sur la courbe,
• une droite passant par A et B.
• Pour aller de A à B, il y a un accroissement Δx et un accroissement Δy
• le rapport Δy/Δx est égal à la pente de la droite. Ce rapport indique la variation de la fonction y = f(x) entre A et B. Mais cette variation n'est pas constante. On peut remarquer, dans l'exemple de la vidéo, que près de A, la fonction varie plus lentement que près de B. Et n'y a-t-il pas de diminution locale, entre les 2 points ? Si on ne connaissait que ce rapport, cela ne permettrait pas de le dire. Pour connaitre la variation de f au voisinage immédiat du point A, on va donc diminuer l'accroissement Δx.
• Lorsqu'on diminue l'accroissement Δx, on voit que la droite AB se rapport de la tangente à la courbe en A.
• Regardez aussi comment varie la pente de cette droite (le rapport Δy/Δx). On voit que ce rapport tend vers la pente de la tangente. C'est la dérivée de f en A.
  f '(x_A) = lim_Δx-->0 (f(x_A + Δx) - f(x_A)) / Δx

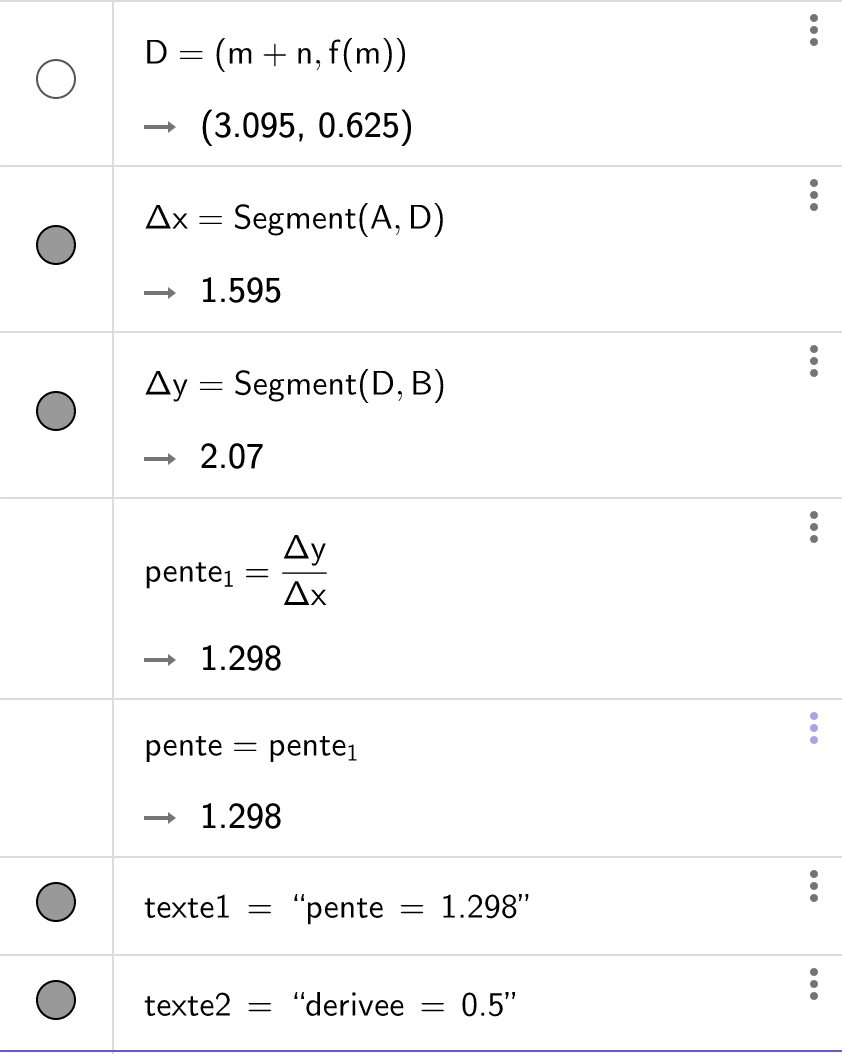
Pour construire vous-même une autre fonction, et/ou chercher la dérivée en un autre point, utilisez GeoGebra (application ou version en ligne), en vous inspirant des éléments ci-dessous.