Fonctions - la parabole

Prérequis

• les fonctions
• résolution d'équations

y = a . x² + b . x + c

où

• x est la variable indépendante,
• y est la variable dépendante, et
• a, b et c sont des constantes (les paramètres de l'équation).

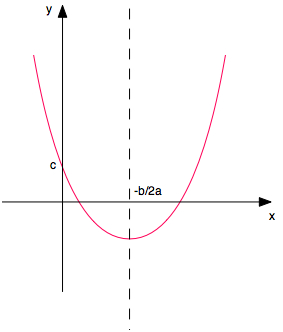
L'équation y = a . x² + b . x + c est l'équation générale d'une parabole.
En remplaçant les lettres a, b et c (les paramètres) par des valeurs, selon ces valeurs, on a différentes paraboles (= équations particulières).

La parabole est tournée vers les y positifs lorsque a > 0 (comme ci-dessus).
Elle possède un axe de symétrie en x = -b/2a.
L'intersection de cet axe avec la parabole est un extremum (maximum ou minimum).
Elle coupe l'axe Y (c.à.d. x = 0) en y = c.
Elle coupe l'axe des X en 0, 1 ou 2 points, appelés les racines (résoudre y = 0 = a . x² + b . x + c pour les trouver).