Dès les débuts de l'étude de l'électricité on s'est posé la question de savoir si la charge électrique est une grandeur qui peut varier de manière continue ou si, au contraire, il existe une sorte d'atome d'"électricité", c-à-d une valeur minimum dont toutes les charges seraient des multiples entiers. En d'autres mots se pose le problème de la quantification de la charge électrique.

Les lois de l'électrolyse établies par Faraday en 1833 laissent prévoir l'existence d'une charge élémentaire; les ions porteraient un nombre entier de ces charges. Vers la fin du dix-neuvième siècle, l'étude des rayons cathodiques et des rayons X laisse entrevoir que l'atome doit être composé de particules portant des charges électriques.
En 1897 J.J. Thomson mesure le rapport e/m de la charge à la masse des ions gazeux.
Mais Millikan est le premier, vers 1910, à mesurer directement des charges très faibles et à établir qu'il existe une charge minimum : l'électron.

Entre deux plaques parallèles, il pulvérise des gouttelettes d'huile d'un rayon de l'ordre du micromètre. Du fait même de la pulvérisation, le frottement charge ces gouttelettes. Elles sont observées au microscope avec un éclairage latéral de telle sorte qu'elles apparaissent sous forme de points brillants sur fond noir et qu'on peut suivre facilement leur déplacement.

1 - Si entre les plaques parallèles il n'y a pas de différence de potentiel, aucune force électrique ne s'exerce sur la gouttelette.

Celle-ci est soumise

• à son poids vers le bas : m . g
• à la poussée d'Archimède vers le haut: ρ_air. V . g
• à la résistance de l'air au cheminement vers le haut :  6 . π . η . v . r 

Elle tombe avec une vitesse limite de sédimentation vers le bas (a = 0, v = constante):

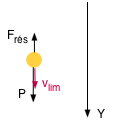
∑ £F = £0 ==> - ρ_air. V . g - 6 . π . η . v_lim . r  + m . g = 0 (axe vertical vers le bas)
==> v_lim = (2/9) . (ρ_huile - ρ_air) . r² .  g / η

où ρ_huile est ici la masse volumique de l'huile
ρ_air celle de l'air
r le rayon de la gouttelette
η le coefficient de viscosité de l'air.

La vitesse peut être déterminée expérimentalement en mesurant le temps que met la gouttelette pour franchir l'espace entre deux fils réticulaires du microscope.
La formule précédente permet ainsi de calculer le rayon de cette gouttelette.

2 - En mettant entre les deux plaques parallèles une différence de potentiel telle que la force électrique exercée sur la gouttelette soit dirigée vers le haut et qu'elle soit supérieure au poids, la gouttelette est soumise aux forces suivantes:

• la force électrique vers le haut : E . q où E est le champ électrique uniforme entre les plaques et q la charge de la goutelette,
• la force de pesanteur vers le bas : m . g
• la poussée d'Archimède vers le haut: ρ_air. V . g
• la force de résistance au cheminement vers le bas :  6 . π . η . v . r 

La gouttelette possède à nouveau une vitesse limite (==> constante ==> a = 0) vers le haut, définie par l'équilibre des forces :

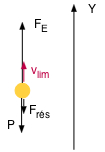
∑ £F = £0 ==> E . q + ρ_air. V . g - m . g - 6 . π . η . v_lim . r = 0 (axe vertical vers le haut)

ce qui permet de déterminer la charge q, toutes les autres grandeurs étant mesurables directement.

3 - Lorsque la gouttelette est arrivée en haut, on supprime la différence de potentiel et elle redescend. On rétablit la différence de potentiel : elle remonte, et ainsi de suite.
Or Millikan remarque que la vitesse ascensionnelle d'une même gouttelette varie d'une fois à l'autre : c'est que sa charge varie par capture d'un ion de l'air.
Si on appelle q₁ et q₂ deux charges successives de la même gouttelette et v₁ et v₂ les vitesses ascensionelles correspondantes, on a

E . q₁ = m . g - ρ_air. V. g + 6 . π . η  . v₁ . r
E . q₂ = m . g - ρ_air. V. g + 6 . π . η v₂ . r
d'où E . (q₁ - q₂) = 6 . π . η . (v₁ - v₂) . r

ce qui permet de déterminer les variations de charge.

L'expérience montre que ces variations de vitesse ne sont pas quelconques mais qu'elles sont toujours des multiples entiers d'un même minimum. On en conclut que les variations de charge sont elles aussi des multiples entiers d'une valeur minimum : la charge de l'électron.

Les mesures ont donné à cette charge de l'électron la valeur