Circuits en courant alternatif

avec différents éléments en série et/ou en parallèle : exemple 2 - R et L en parallèle

Soit un circuit comprenant une résistance et une self en parallèle.

1. Quel est la grandeur commune à ces deux éléments ? C'est E.
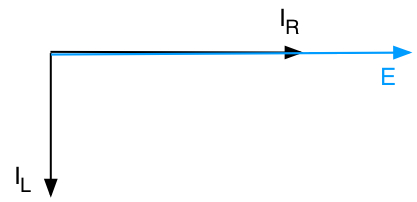
   On représente E par un vecteur horizontal vers la droite.

   

2. On représente les autres grandeurs, à savoir les différents I_i : I_R et I_L.

   • Pour une résistance, le E est en phase avec le I.
   • Pour une self, le E est en avance de 90° sur le I, donc I est en retard de 90° sur E.

   

3. On fait la somme vectorielle de ces deux I_i.

   

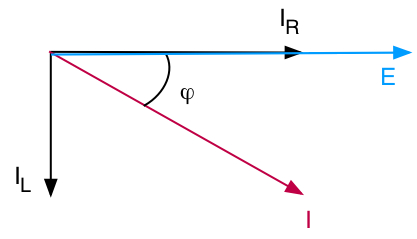
4. On fait les calculs de I et φ en utilisant :

   1. la trigonométrie appliquée à cette représentation de Fresnel,
      \( \class{formule}{ I = \sqrt{I_R^2 + I_L^2} }\)
      \( \class{formule}{ tgφ = \dfrac{I_L}{I_R} }\)

   2. les impédances individuelles:  Z_R = R, Z_L = L . ω

   3. la loi d'Ohm généralisée : E = Z_R . I_R, E = Z_L . I_L

      ⇒ \( \class{formule}{ I = \sqrt{ (\dfrac{E}{R})^2 + (\dfrac{E}{L . ω})^2} = E . \sqrt{ (\dfrac{1}{R})^2 + (\dfrac{1}{L . ω})^2} }\)

      et \( \class{formule}{ tgφ = \dfrac{I_L}{I_R} = \dfrac{(E / L . ω)}{(E / R)} = \dfrac{R}{L . ω} }\) ⇒ \( \class{formule}{ φ = arctg\dfrac{R}{L . ω} }\)

      Pour Z, \( \class{formule}{ Z = \dfrac{E}{I} = \dfrac{1}{\sqrt{(1/R)^2 + (1/L . ω)^2}} }\)