Si on suppose que la bobine est concentrée, tous ses conducteurs sont localisés en  (figure 6). Le théorème d'Ampère appliqué à tout contour qui traverse l'entrefer sans encercler la bobine (contour 1 à la figure 6, traversant l'entrefer en (figure 6). Le théorème d'Ampère appliqué à tout contour qui traverse l'entrefer sans encercler la bobine (contour 1 à la figure 6, traversant l'entrefer en 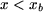 ) fournit : ) fournit :
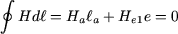 |
(21) |
Le théorème d'Ampère appliqué à un contour qui traverse l'entrefer en encerclant la bobine (contour 2 à la figure 6, traversant l'entrefer en 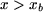 ) fournit : ) fournit :
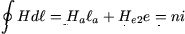 |
(22) |
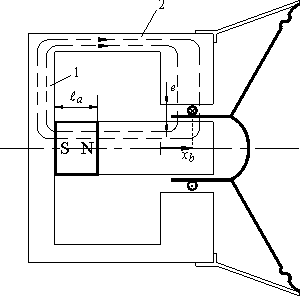
Figure 6
Pour obtenir la valeur de  , on doit, comme on l'a fait dans le cas du calcul du champ dû à l'aimant, utiliser la conservation du flux : , on doit, comme on l'a fait dans le cas du calcul du champ dû à l'aimant, utiliser la conservation du flux :
- le flux à travers l'entrefer vaut :
- le flux à travers l'aimant vaut :
Comme on doit avoir 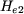 , il vient : , il vient :
 |
(23) |
Des équations (21), (22) et (23), on peut déduire la valeur du champ 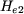 : :
 |
(24) |
Le flux intercepté par la bobine est égal à  fois le flux traversant l'entrefer de fois le flux traversant l'entrefer de 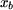 à à 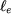
 |
(25) |
On a, compte tenu de (24)
 |
(26) |
L'inductance  de la bobine est donc égale à : de la bobine est donc égale à :
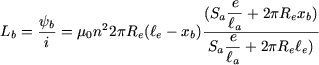 |
(27) |
La force du type reluctant qui s'exerce sur la bobine vaut :
 |
(28) |
Cette force, qui fait apparaître un terme non linéaire dans la relation qui lie la force totale s'exerçant sur la bobine mobile au courant qui y circule, est généralement rendue négligeable devant la force d'origine électrodynamique par un dimensionnement adéquat du dispositif. C'est pourquoi en général, seul le terme de type électrodynamique est pris en compte.
|