Deux méthodes de calcul peuvent être utilisées pour calculer la force d'origine électrodynamique qui s'exerce sur la bobine dans le sens des  positifs. La première est basée sur la loi positifs. La première est basée sur la loi 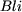 puisque les conducteurs qui forment la bobine sont soumis au champ d'entrefer puisque les conducteurs qui forment la bobine sont soumis au champ d'entrefer  . La deuxième est basée sur le calcul de la variation de la coénergie en fonction de la position. . La deuxième est basée sur le calcul de la variation de la coénergie en fonction de la position.
1ère méthode
Pour calculer la valeur du champ  en tout point de l'entrefer, on utilise le théorème d'Ampère appliqué à un contour traversant radialement l'entrefer et axialement l'aimant (figure 3). On a en tout point de l'entrefer, on utilise le théorème d'Ampère appliqué à un contour traversant radialement l'entrefer et axialement l'aimant (figure 3). On a
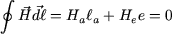 |
(1) |
puisqu'on suppose que :
- la perméabilité du fer est infinie et donc que le champ
 dans le fer est nul dans le fer est nul
- le champ
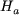 dans l'aimant est uniforme et purement axial. dans l'aimant est uniforme et purement axial.
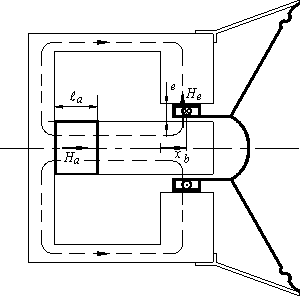
Figure 3
On déduit de (1) que le champ 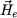 a la même valeur a la même valeur 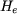 en tout point de l'entrefer et que cette valeur est égale à en tout point de l'entrefer et que cette valeur est égale à
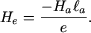 |
(2) |
Du champ 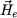 dans l'entrefer on passe à la valeur du champ dans l'entrefer on passe à la valeur du champ 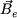 par la relation par la relation 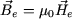 . .
Le flux y qui traverse l'entrefer est égal à
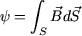 |
(3) |
Comme 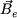 est purement radial et de valeur constante en tout point de l'entrefer, on a : est purement radial et de valeur constante en tout point de l'entrefer, on a :
 |
(4) |
Le flux y se referme à travers le noyau et l'aimant. Le flux à travers l'aimant vaut 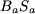 , où , où 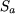 est la section droite de l'aimant (égale à est la section droite de l'aimant (égale à 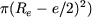 ); d'où : ); d'où :
 |
(5) |
On en déduit la relation suivante :
 |
(6) |
En combinant (6) avec (2), on a, compte tenu de ce que 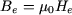 : :
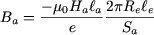 |
(7) |
L'équation (7) fournit une relation liant 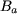 à à 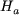 . .
On dispose d'une deuxième relation qui est la caractéristique 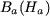 de l'aimant de l'aimant
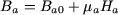 |
(8) |
D'où, au point de fonctionnement correspondant à l'intersection des deux droites données par (7) et (8) (cf. figure 4) :
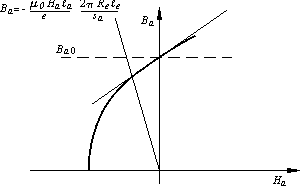
Figure 4
 |
(9) |
et donc
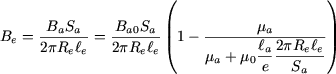 |
(10) |
Si le courant i qui y circule est considéré comme positif lorsqu'il traverse le plan de coupe de la figure 1 comme indiqué (c'est-à-dire de l'avant vers l'arrière dans la partie située au-dessus de l'axe de symétrie, de l'arrière vers l'avant dans la partie située en-dessous), la force 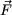 d'origine électrodynamique que développe dans le sens des d'origine électrodynamique que développe dans le sens des  positifs une spire vaut : positifs une spire vaut :
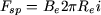 |
(11) |
où 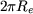 est la longueur de la spire. est la longueur de la spire.
Comme la bobine comporte  spires, la force totale spires, la force totale 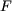 est égale à : est égale à :
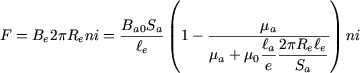 |
(12) |
2ème méthode
Le calcul du champ d'entrefer 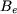 s'opère de la même manière que pour la première méthode. En tout point de l'entrefer le champ s'opère de la même manière que pour la première méthode. En tout point de l'entrefer le champ 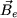 est radial et sa valeur est égale à (figure 1) : est radial et sa valeur est égale à (figure 1) :
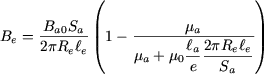 |
(13) |
Le flux dû à l'aimant qui traverse une section droite du noyau située en  , ( , (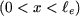 ) est égal au flux qui traverse l'entrefer de ) est égal au flux qui traverse l'entrefer de  à à 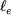 (figure 5) : (figure 5) :
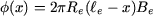 |
(14) |
Figure 5
Il circule dans le sens des  positifs. Ce flux est au signe près le flux dû à l'aimant qui traverse une spire du bobinage lorsqu'elle est située à la même position, si on choisit comme sens positif de parcours du courant celui indiqué à la figure 2. positifs. Ce flux est au signe près le flux dû à l'aimant qui traverse une spire du bobinage lorsqu'elle est située à la même position, si on choisit comme sens positif de parcours du courant celui indiqué à la figure 2.
Le flux y0 à travers la bobine vaut, lorsque son point milieu occupe une position 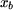 (figure 3) : (figure 3) :
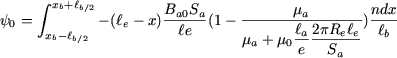 |
(15) |
Ceci donne
 |
(16) |
Le flux total induit dans la bobine est égal à :
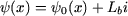 |
(17) |
où 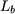 est l'inductance propre de la bobine. Par analogie avec (2.45) (cf. chapitre 2, § 2.6 du livre) la coénergie magnétique s'écrit : est l'inductance propre de la bobine. Par analogie avec (2.45) (cf. chapitre 2, § 2.6 du livre) la coénergie magnétique s'écrit :
 |
(18) |
Le terme  qui est égal à la coénergie à courant nulle (ou encore à l'opposé de l'énergie magnétique stockée à courant nul) est un terme indépendant de la position de la bobine mobile puisque le circuit magnétique vu par l'aimant est invariant vis-à-vis de la position de celle-ci. qui est égal à la coénergie à courant nulle (ou encore à l'opposé de l'énergie magnétique stockée à courant nul) est un terme indépendant de la position de la bobine mobile puisque le circuit magnétique vu par l'aimant est invariant vis-à-vis de la position de celle-ci.
La force qui s'exerce sur la bobine qui s'écrit comme étant la dérivée partielle de la coénergie par rapport à la position de la bobine vaut donc :
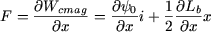 |
(19) |
Le terme  correspond à la force électrodynamique. Le terme correspond à la force électrodynamique. Le terme 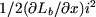 correspond à la force d'origine réluctante. correspond à la force d'origine réluctante.
La force d'origine électrodynamique vaut :
 |
(20) |
On constate que la relation (20) qu'on vient d'établir fournit la même valeur que le calcul à partir de la règle  . .
|