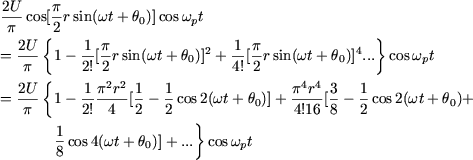<< Retour à l'énoncé |

En regroupant dans le facteur qui multiplie les termes constants, les termes en , les termes en , ... on a :

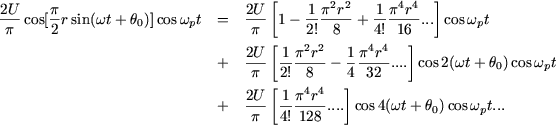Comme , il vient finalement :

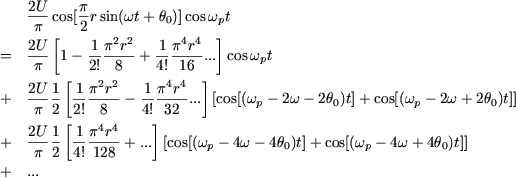Le terme de pulsation et d'amplitude est donc bien équivalent à un ensemble de raies :

• une de pulsation

• deux de pulsations et ayant toutes les deux la même amplitude

• deux de pulsations et ayant toutes les deux la même amplitude

• ...

Les amplitudes des raies décroissent rapidement à mesure que leur pulsation s'écarte de la pulsation w_p.

· Par un calcul similaire, on montre que le terme de pulsation du pseudo développement en série de Fourier

donne :

• deux raies de pulsations et ayant toutes les deux la même amplitude

• deux raies de pulsations et ayant toutes les deux la même amplitude

• ...

Les harmoniques se groupent en famille situées autour des pulsations , , ,...

<< Retour à l'énoncé |